题目内容
17.2014年第二届夏季青年奥林匹克运动会将在中国南京举行,为了迎接这一盛会,某公司计划推出系列产品,其中一种是写有“青奥吉祥数”的卡片.若设正项数列{an}满足n(n+1)an2-an-1=0,定义使log2ak为整数的实数k为“青奥吉祥数”,则在区间[1,2014]内的所有“青奥吉祥数之和”为2047.分析 正项数列{an}满足n(n+1)an2-an-1=0,可得${a}_{n}=\frac{1}{n}$,log2ak=$lo{g}_{2}\frac{1}{k}$=-log2k=m∈Z,k=2-m∈[1,2014],解得m=0,-1,-2,…,-10.再利用等比数列的前n项和公式即可得出.
解答 解:∵正项数列{an}满足n(n+1)an2-an-1=0,
∴(nan-1)[(n+1)an+1]=0,∴${a}_{n}=\frac{1}{n}$,
∴log2ak=$lo{g}_{2}\frac{1}{k}$=-log2k=m∈Z,k=2-m∈[1,2014],解得m=0,-1,-2,…,-10.
∴在区间[1,2014]内的所有“青奥吉祥数之和”S=2°+21+22+…+210=$\frac{{2}^{11}-1}{2-1}$=2047.
故答案为:2047.
点评 本题考查了递推式、对数的运算性质、等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.已知α,β是两个平面,直线l?α,l?β,若以①l⊥α,②l∥β,③α⊥β中两个为条件,另一个为结论构成三个命题,其中 正确的命题是( )
| A. | ①③⇒②,①②⇒③ | B. | ①③⇒②,②③⇒① | C. | ①②⇒③,②③⇒① | D. | ①③⇒②,①②⇒③,②③⇒① |
7.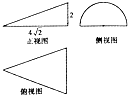 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )| A. | 16$\sqrt{2}$+16π | B. | 16$\sqrt{2}$+8π | C. | 8$\sqrt{2}$+8π | D. | 8$\sqrt{2}$+16π |