题目内容
已知函数f(x) =2lnx-x2
(I)若方程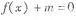 在[
在[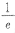 ,e]内有两个不等的实根,求实数m的取值范围(e为自然对数的底数);
,e]内有两个不等的实根,求实数m的取值范围(e为自然对数的底数);
(II)如果函数,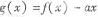 的图象与-轴交于两点力(
的图象与-轴交于两点力(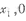 ),B(
),B(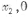 ),且
),且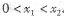
求证: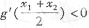 (其中
(其中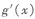 为
为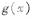 的导函数).
的导函数).
(I)若方程
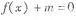 在[
在[ ,e]内有两个不等的实根,求实数m的取值范围(e为自然对数的底数);
,e]内有两个不等的实根,求实数m的取值范围(e为自然对数的底数);(II)如果函数,
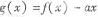 的图象与-轴交于两点力(
的图象与-轴交于两点力(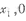 ),B(
),B(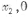 ),且
),且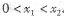
求证:
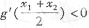 (其中
(其中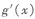 为
为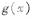 的导函数).
的导函数).解:(Ⅰ)由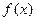 =2
=2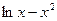 ,求导得
,求导得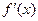 =
= , ……2分
, ……2分
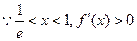 ;
;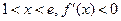 ,
,
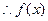 在
在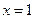 处取得极大值
处取得极大值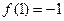 . ……4分
. ……4分
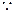

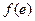 =2―
=2―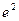 ,
,
且知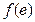 <
<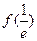 ,故
,故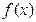 =-
=-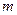 ,在
,在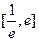 内有两个不等的实根满足:
内有两个不等的实根满足:
-2-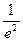 ≤-
≤-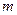 <-1,故
<-1,故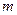 的取值范围为
的取值范围为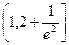 . ………6分
. ………6分
(Ⅱ)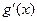 =
=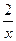 -2
-2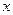 -
-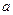 ,
,
又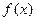 -
-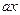 =0有两个不等的实根
=0有两个不等的实根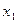 、
、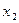 ,则
,则

两式相减得到
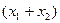 , …………8分
, …………8分
于是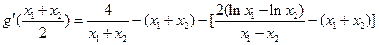 =
=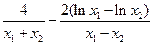 .
.
要证: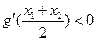 ,只需证:
,只需证: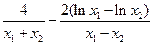 <
< 0,
0,
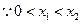 ,只需证:
,只需证: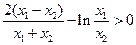 .
.
令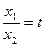 ,0
,0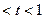 ,只需证:
,只需证: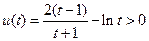 在
在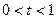 上恒成立,…10分
上恒成立,…10分
又∵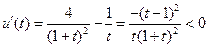 ,∴
,∴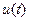 在
在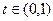 上为减函数,
上为减函数,
则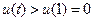 ,从而知
,从而知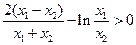 ,
,
从而原不等式成立. …………12分
…………12分
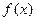 =2
=2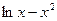 ,求导得
,求导得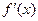 =
= , ……2分
, ……2分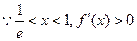 ;
;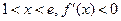 ,
,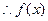 在
在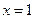 处取得极大值
处取得极大值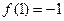 . ……4分
. ……4分

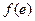 =2―
=2―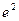 ,
, 且知
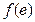 <
<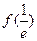 ,故
,故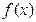 =-
=-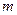 ,在
,在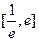 内有两个不等的实根满足:
内有两个不等的实根满足:-2-
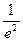 ≤-
≤-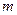 <-1,故
<-1,故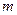 的取值范围为
的取值范围为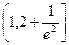 . ………6分
. ………6分(Ⅱ)
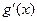 =
=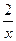 -2
-2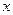 -
-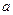 ,
, 又
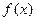 -
-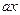 =0有两个不等的实根
=0有两个不等的实根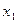 、
、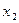 ,则
,则
两式相减得到

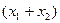 , …………8分
, …………8分于是
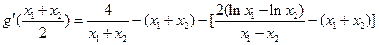 =
=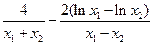 .
.要证:
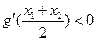 ,只需证:
,只需证: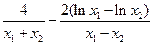 <
< 0,
0,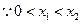 ,只需证:
,只需证: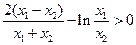 .
.令
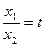 ,0
,0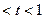 ,只需证:
,只需证: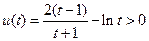 在
在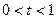 上恒成立,…10分
上恒成立,…10分又∵
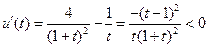 ,∴
,∴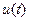 在
在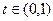 上为减函数,
上为减函数, 则
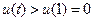 ,从而知
,从而知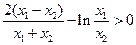 ,
,从而原不等式成立.
 …………12分
…………12分略

练习册系列答案
相关题目
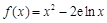 .(
.(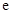 为自然对数的底)
为自然对数的底)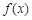 的最小值;
的最小值;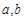 使得
使得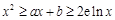 对于任意的正数
对于任意的正数 恒成立?若存在,求出
恒成立?若存在,求出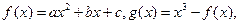 (
(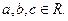 )若
)若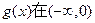 上是增函数,在(0,1)上是减函数,函数
上是增函数,在(0,1)上是减函数,函数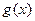 在R上有三个零点,且1是其中一个零点。
在R上有三个零点,且1是其中一个零点。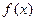 最小值的取值范围。
最小值的取值范围。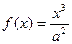 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为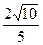 ,函数
,函数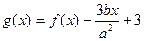 。
。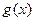 在
在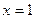 处有极值,求
处有极值,求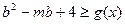 在
在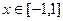 时恒成立,求实数
时恒成立,求实数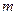 的取值范围。
的取值范围。 函数
函数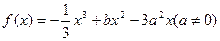 在
在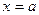 处取得极值.
处取得极值.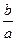 ;
;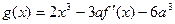 ,如果
,如果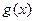 在开区间
在开区间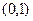 上存在极小值,求实数
上存在极小值,求实数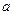 的取值范围.
的取值范围.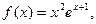
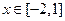 的最大值为 。
的最大值为 。 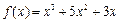 在区间
在区间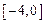 上的最大值是 .
上的最大值是 .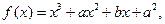 在
在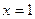 时有极值
时有极值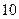 ,那么
,那么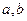 的值分别为_______
的值分别为_______ 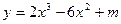 (m
(m 为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .
为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .