题目内容
(本题满分12分)已知函数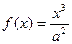 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为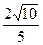 ,函数
,函数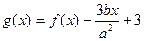 。
。
(1)若函数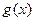 在
在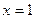 处有极值,求
处有极值,求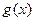 的解析式;
的解析式;
(2)若函数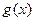 在区间[-1,1]上为增函数,且
在区间[-1,1]上为增函数,且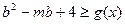 在
在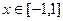 时恒成立,求实数
时恒成立,求实数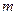 的取值范围。
的取值范围。
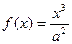 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为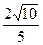 ,函数
,函数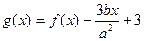 。
。(1)若函数
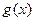 在
在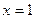 处有极值,求
处有极值,求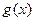 的解析式;
的解析式;(2)若函数
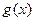 在区间[-1,1]上为增函数,且
在区间[-1,1]上为增函数,且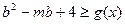 在
在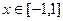 时恒成立,求实数
时恒成立,求实数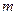 的取值范围。
的取值范围。(1)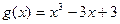
(2)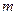 的取值范围是
的取值范围是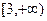
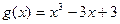
(2)
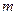 的取值范围是
的取值范围是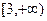
(1)∵ ,∴由
,∴由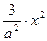 =3得
=3得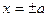 ,
,
即切点坐标为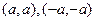
∴切线方程为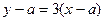 ,或
,或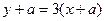 2分
2分
整理得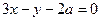 或
或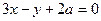
∴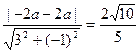 ,解得
,解得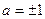 ,∴
,∴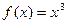 。
。
∴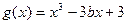 4分
4分
∵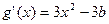 ,
,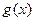 在
在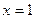 处有极值,∴
处有极值,∴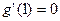 ,
,
即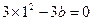 ,解得
,解得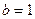
∴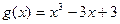 6分
6分
(2)∵函数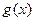 在区间[-1,1]上为增函数,
在区间[-1,1]上为增函数,
∴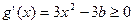 在区间[-1,1]上恒成立,
在区间[-1,1]上恒成立,
∴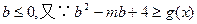 在区间[-1,1]上恒成立,
在区间[-1,1]上恒成立,
∴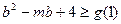 8分
8分
即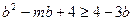 ,若
,若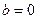 ,则不等式显然成立,若
,则不等式显然成立,若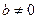 ,
,
则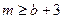 在
在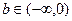 上恒成立,∴
上恒成立,∴
故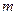 的取值范围是
的取值范围是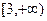 12分
12分
 ,∴由
,∴由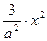 =3得
=3得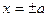 ,
,即切点坐标为
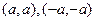
∴切线方程为
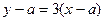 ,或
,或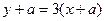 2分
2分整理得
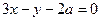 或
或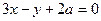
∴
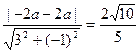 ,解得
,解得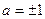 ,∴
,∴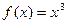 。
。∴
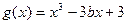 4分
4分∵
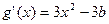 ,
,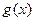 在
在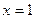 处有极值,∴
处有极值,∴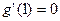 ,
,即
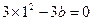 ,解得
,解得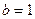
∴
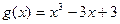 6分
6分(2)∵函数
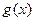 在区间[-1,1]上为增函数,
在区间[-1,1]上为增函数,∴
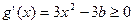 在区间[-1,1]上恒成立,
在区间[-1,1]上恒成立,∴
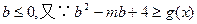 在区间[-1,1]上恒成立,
在区间[-1,1]上恒成立,∴
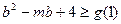 8分
8分即
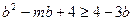 ,若
,若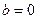 ,则不等式显然成立,若
,则不等式显然成立,若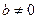 ,
,则
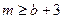 在
在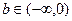 上恒成立,∴
上恒成立,∴
故
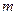 的取值范围是
的取值范围是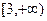 12分
12分
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
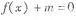 在[
在[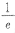 ,e]内有两个不等的实根,求实数m的取值范围(e为自然对数的底数);
,e]内有两个不等的实根,求实数m的取值范围(e为自然对数的底数);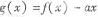 的图象与-轴交于两点力(
的图象与-轴交于两点力(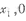 ),B(
),B(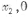 ),且
),且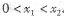
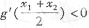 (其中
(其中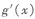 为
为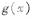 的导函数).
的导函数).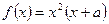 .
.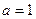 时,求
时,求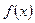 的极值;
的极值;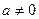 时,求
时,求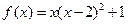 ,
,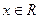
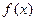 的极值;
的极值;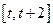 上的最大值.
上的最大值.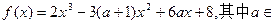 R.
R.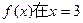 处取得极值,求常数
处取得极值,求常数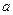 的值;
的值;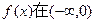 上为增函数,求
上为增函数,求 (a>0,x∈R).
(a>0,x∈R). 递减,求实数a的取值范围;
递减,求实数a的取值范围;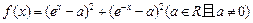 ,求
,求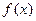 的最小值.
的最小值. 的图象,给出下列命题:
的图象,给出下列命题: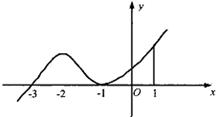
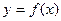 的极值点;
的极值点;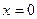 处切线的斜率小于零;
处切线的斜率小于零;