题目内容
函数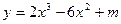 (m
(m 为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .
为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .
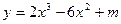 (m
(m 为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .
为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .-37
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
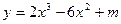 (m
(m 为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .
为常数)在[-2,2]上的最大值为3,那么此函数在[-2,2]上的最小值为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案