题目内容
函数y=x2cosx的导数为( ).
| A.y′=2xcosx-x2sinx | B.y′=2xcosx+x2sinx |
| C. y′=x2cosx-2xsinx | D.y′=xcosx-x2sinx |
A
解析试题分析:因为y=x2cosx,所以, ,故选A。
,故选A。
考点:本题主要考查导数的计算。
点评:简单题,利用函数乘积的导数运算法则,以及幂函数、余弦函数的导数公式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个物体的运动方程为 ,其中
,其中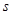 的单位是米,
的单位是米,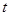 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
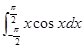 的值为 ( )
的值为 ( )
| A.0 | B.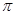 | C.2 | D.-2 |
函数 有小于1的极值点,则实数
有小于1的极值点,则实数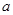 的取值范围是( )
的取值范围是( )
A.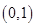 | B.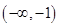 | C. | D.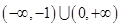 |
曲线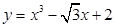 上的任意一点P处切线的斜率的取值范围是( )
上的任意一点P处切线的斜率的取值范围是( )
A.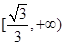 | B.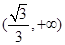 | C.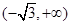 | D.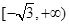 |
若 ,则
,则 ( )
( )
| A.0 | B.1 | C.2 | D.3 |
已知 =
= ·
·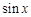 ,则
,则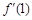 =( )
=( )
A.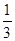 + cos1 + cos1 | B.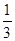 sin1+cos1 sin1+cos1 | C.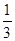 sin1-cos1 sin1-cos1 | D.sin1+cos1 |
三次函数当 时有极大值
时有极大值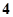 ,当
,当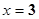 时有极小值
时有极小值 ,且函数过原点,则此函数是( )
,且函数过原点,则此函数是( )
A.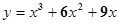 | B.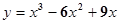 |
C. | D.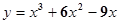 |
设连续函数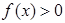 ,则当
,则当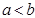 时,定积分
时,定积分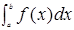 的符号
的符号
| A.一定是正的 |
| B.一定是负的 |
C.当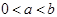 时是正的,当 时是正的,当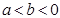 时是负的 时是负的 |
| D.以上结论都不对 |