题目内容
一个物体的运动方程为 ,其中
,其中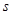 的单位是米,
的单位是米,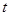 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
A
解析试题分析:因为 ,所以
,所以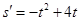 ,所以在3秒末的瞬时速度为
,所以在3秒末的瞬时速度为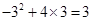 米/秒.
米/秒.
考点:本小题主要考查导数在物理中的应用.
点评:路程函数在某一时刻的导数即为该物体在那一时刻的瞬时速度.

练习册系列答案
相关题目
若存在过点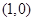 的直线与曲线
的直线与曲线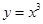 和
和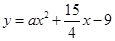 都相切,则
都相切,则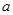 等于
等于
A.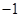 或 或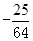 | B.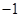 或 或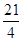 | C.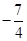 或 或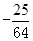 | D.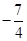 或 或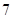 |
“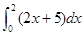 等于
等于
| A.9 | B.11 | C.14 | D.18 |
若实数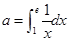 .则函数
.则函数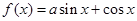 的图像的一条对称轴方程为
的图像的一条对称轴方程为
| A.x=0 | B.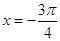 | C.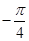 | D.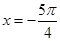 |
 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若 ,
, 满足
满足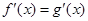 ,则
,则 与
与 满足
满足
A.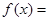  | B.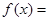 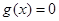 |
C.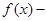  为常数函数 为常数函数 | D.  为常数函数 为常数函数 |
计算定积分 的值是( )
的值是( )
A.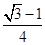 | B.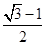 | C.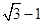 | D.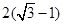 |
曲线y=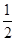 x2-2x在点
x2-2x在点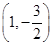 处的切线的倾斜角为( ).
处的切线的倾斜角为( ).
| A.-135° | B.45° | C.-45° | D.135° |
若函数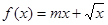 在区间
在区间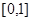 单调递增,则m的取值范围为
单调递增,则m的取值范围为
A.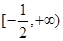 | B.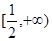 | C.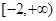 | D.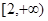 |
函数y=x2cosx的导数为( ).
| A.y′=2xcosx-x2sinx | B.y′=2xcosx+x2sinx |
| C. y′=x2cosx-2xsinx | D.y′=xcosx-x2sinx |