题目内容
三次函数当 时有极大值
时有极大值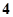 ,当
,当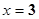 时有极小值
时有极小值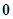 ,且函数过原点,则此函数是( )
,且函数过原点,则此函数是( )
A.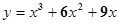 | B.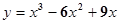 |
C. | D.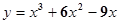 |
B
解析试题分析:本题是据题意求参数的题,题目中x=1时有极大值4,当x=3时有极小值0,且函数图象过原点,可转化出五个等式,则其四建立方程.解:f’(x)=3a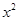 +2bx+c(a≠0),∵x=1时有极大值4,当x=3时有极小值0,∴f’(1)="3a+2b+c=0" ①f’(3)="27a+6b+c=0" ②f(1)="a+b+c+d=4" ③又函数图象过原点,所以 d="0" ④,①②③④联立得 a=1,b=-6,c=9,故函数f(x)=
+2bx+c(a≠0),∵x=1时有极大值4,当x=3时有极小值0,∴f’(1)="3a+2b+c=0" ①f’(3)="27a+6b+c=0" ②f(1)="a+b+c+d=4" ③又函数图象过原点,所以 d="0" ④,①②③④联立得 a=1,b=-6,c=9,故函数f(x)=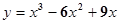 ,故选B.
,故选B.
考点:导数的运用
点评:本小题考点是导数的运用,考查导数与极值的关系,本题的特点是用导数一极值的关建立方程求参数---求函数的表达式

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
若函数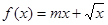 在区间
在区间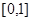 单调递增,则m的取值范围为
单调递增,则m的取值范围为
A.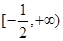 | B.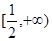 | C.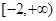 | D.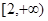 |
函数y=x2cosx的导数为( ).
| A.y′=2xcosx-x2sinx | B.y′=2xcosx+x2sinx |
| C. y′=x2cosx-2xsinx | D.y′=xcosx-x2sinx |
如图是导函数 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )
A.导函数 在 在 处有极小值 处有极小值 |
B.导函数 在 在 处有极大值 处有极大值 |
C.函数 在 在 处有极小值 处有极小值 |
D.函数 在 在 处有极小值 处有极小值 |
.设三次函数 的导函数为
的导函数为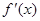 ,函数
,函数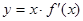 的图象的一部分如图所示,则正确的是
的图象的一部分如图所示,则正确的是 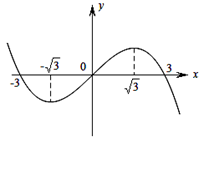
A. 的极大值为 的极大值为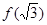 ,极小值为 ,极小值为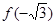 |
B. 的极大值为 的极大值为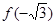 ,极小值为 ,极小值为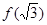 |
C. 的极大值为 的极大值为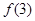 ,极小值为 ,极小值为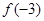 |
D. 的极大值为 的极大值为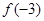 ,极小值为 ,极小值为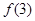 |
如果 为偶函数,且
为偶函数,且 导数存在,则
导数存在,则 的值为( )
的值为( )
| A.0 | B.1 | C.2 | D. |
已知函数 的导函数
的导函数 的图象如图所示,则关于函数
的图象如图所示,则关于函数 ,下列说法正确的是
,下列说法正确的是
A.在 处取得极大值 处取得极大值 |
B.在区间 上是增函数 上是增函数 |
C.在 处取得极大值 处取得极大值 |
D.在区间 上是减函数 上是减函数 |
 =( )
=( )
A. | B.2 | C. | D. |
 是定义域为R的奇函数,且
是定义域为R的奇函数,且 ,
, 的图象如图所示。若正数
的图象如图所示。若正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )



