题目内容
【题目】每年的三月十二日,是中国的植树节,林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两批树苗中各抽测了10株树苗的高度,规定高于128厘米的为“良种树苗”,测得高度如下(单位:厘米)
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两批树苗的高度作比较,写出对两种树苗高度的统计结论;
(2)设抽测的10株甲种树苗高度平均值为 ![]() ,将这10株树苗的高度依次输入按程序框图进行运算,
,将这10株树苗的高度依次输入按程序框图进行运算,
(如图)问输出的S大小为多少?并说明S的统计学意义.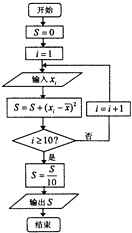
【答案】
(1)解:茎叶图略.统计结论:①甲种树苗的平均高度小于乙种树苗的平均高度;②甲种树苗比乙种树苗长得更整齐;③甲种树苗的中位数为127,乙种树苗的中位数为128.5;④甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散.
(2)解: ![]() .,
.,
S表示10株甲树苗高度的方差,是描述树苗高度离散程度的量.S值越小,表示长得越整齐,S值越大,表示长得越参差不齐.
【解析】(1)将数据填入茎叶图,然后计算两组数据的平均数进行比较,计算中位数从而可得甲、乙两种树苗高度的统计结论;(2)根据流程图的含义可知S表示10株甲树苗高度的方差,是描述树苗高度离散程度的量,根据方差公式解之可得S.
【考点精析】通过灵活运用茎叶图和平均数、中位数、众数,掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据即可以解答此题.

 53随堂测系列答案
53随堂测系列答案【题目】对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如表所示:
分值 | [0,10) | [10,20) | [20,30) | [30,40) |
场数 | 10 | 20 | 40 | 30 |
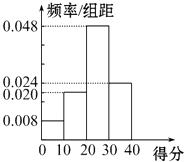
(1)估计甲在一场比赛中得分大于等于20分的概率.
(2)判断甲、乙两名运动员哪个成绩更稳定.(结论不要求证明)
(3)试利用甲的频率分布直方图估计甲每场比赛的平均得分.