Question

【题目】如图，将自然数按如下规则“放置”在平面直角坐标系中，使其满足条件：①每个自然数“放置”在一个“整点”（横纵坐标均为整数的点）上；②0在原点，1在（0，1）点，2在（1，1）点，3在（1，0）点，4在（1，﹣1）点，5在（0，﹣1）点，…，即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上，则放置数字（2n+1）2 ， n∈N*的整点坐标是 ．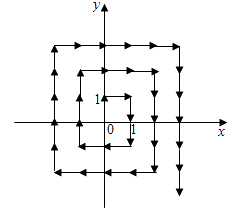

Answer 1

【答案】（﹣n，n+1）
【解析】解：观察已知中点（0，1）处标1，即12 ，
点（﹣1，2）处标9，即32 ，
点（﹣2，3）处标25，即52 ，
…
由此推断
点（﹣n，n+1）处标（2n+1）2 ，
故放置数字（2n+1）2 ， n∈N*的整点坐标是（﹣n，n+1）．
所以答案是：（﹣n，n+1）
【考点精析】利用归纳推理对题目进行判断即可得到答案，需要熟知根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理．