��Ŀ����
����Ŀ���Լס������������˶�Ա�ֱ���100�������еĵ÷��������ͳ�ƣ������ĵ÷�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���г��ҵĵ÷�ͳ�Ʊ������ʾ��
��ֵ | [0��10�� | [10��20�� | [20��30�� | [30��40�� |
���� | 10 | 20 | 40 | 30 |
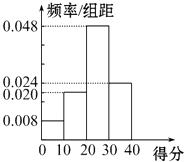
��1�����Ƽ���һ�������е÷ִ��ڵ���20�ֵĸ��ʣ�
��2���жϼס��������˶�Ա�ĸ��ɼ����ȶ��������۲�Ҫ��֤����
��3�������ü�Ƶ�ʷֲ�ֱ��ͼ���Ƽ�ÿ��������ƽ���÷֣�
���𰸡�
��1���⣺����Ƶ�ʷֲ�ֱ��ͼ��֪����һ�������е÷ִ��ڵ��ڣ�20�֣���Ƶ��Ϊ0.048��10+0.024��10=0.48+0.24=0.72��
������һ�������е÷ֲ����ڣ�20�֣��ĸ���Ϊ0.72
��2���⣺���ݼ�Ƶ�ʷֲ�ֱ��ͼ��֪���ijɼ���Ҫ������[20��30�����ҵijɼ��ȽϷ�ɢ�����Լ��ȶ���
��3���⣺��Ϊ���Ϊ10�����Լ�������[0��10����[10��20����[20��30����[30��40���ϵ÷�Ƶ��ֵ�ֱ�Ϊ ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
���ƽ���÷�ΪS����S= ![]() ��5��8+15��20+25��48+35��24��=23.80
��5��8+15��20+25��48+35��24��=23.80
����������1������Ƶ�ʷֲ�ֱ��ͼ���������һ�������е÷ֲ�����20�ֵ�Ƶ�ʼ��ɣ���2�����ݼ����˶�Ա�÷ֵķֲ�����������жϼס��������˶�Ա�ɼ��ȶ����ȶ��ԣ���3������ƽ�����ļ��㹫ʽ�����ɵõ����ۣ�
�����㾫�������ڱ��⿼���Ƶ�ʷֲ�ֱ��ͼ��ƽ��������λ������������Ҫ�˽�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ����ƽ��������������λ����������һ�����ݼ������Ƶ�������ƽ��������������λ�����е�λ����ƽ������ӳһ�����ݵ�ƽ��ˮƽ�������������е�ÿ�������й�ϵ��������Ϊ��Ҫ��Ӧ����㣻����λ�����ܸ���ƫ���ƫС���ݵ�Ӱ�죻��������������ݳ��ֵ�Ƶ���йأ����ܸ������ݵ�Ӱ�죬��ʱ��������Ϊ���ĵ����ݲ��ܵó���ȷ�𰸣�

 ��У����ϵ�д�
��У����ϵ�д�