题目内容
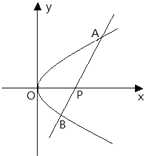
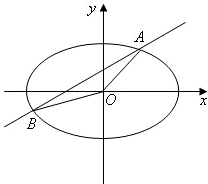
如图,已知椭圆E1方程为
+
=1(a>b>0),圆E2方程为x2+y2=a2,过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C.
(Ⅰ)若k1=1时,B恰好为线段AC的中点,试求椭圆E1的离心率e;
(Ⅱ)若椭圆E1的离心率e=
,F2为椭圆的右焦点,当|BA|+|BF2|=2a时,求k1的值;
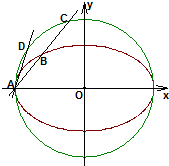
(Ⅲ)设D为圆E2上不同于A的一点,直线AD的斜率为k2,当
=
时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)若k1=1时,B恰好为线段AC的中点,试求椭圆E1的离心率e;
(Ⅱ)若椭圆E1的离心率e=
| 1 |
| 2 |
(Ⅲ)设D为圆E2上不同于A的一点,直线AD的斜率为k2,当
| k1 |
| k2 |
| b2 |
| a2 |

(I)当k1=1时,点C在y轴上,且C(0,a),则B(-
,
),
由点B在椭圆上,得
+
=1,化为
=
,
∴e=
=
=
.
(II)设椭圆的作焦点为F1,由椭圆的定义可知:|BF1|+|BF2|=2a,又|BA|+|BF2|=2a,
∴|BF1|=|BA|,则点B在线段AF1的垂直平分线上,
∴xB=-
,
又e=
=
,∴c=
a,b=
a,
∴xB=-
a,代入椭圆方程得yB=±
b=±
a,
∴k1=
=±
.
(III)直线BD过定点(a,0),证明如下:
设P(a,0),B(xB,yB),则
+
=1(a>b>0).
则kAD•kPB=
k1kPB=
•
•
=
•
=
×(-
)=-1.
∴PB⊥AD,又PD⊥AD,
∴三点P,B,D共线,即直线BD过定点P(a,0).
| a |
| 2 |
| a |
| 2 |
由点B在椭圆上,得
(-
| ||
| a2 |
(
| ||
| b2 |
| b2 |
| a2 |
| 1 |
| 3 |
∴e=
| c |
| a |
1-
|
| ||
| 3 |
(II)设椭圆的作焦点为F1,由椭圆的定义可知:|BF1|+|BF2|=2a,又|BA|+|BF2|=2a,
∴|BF1|=|BA|,则点B在线段AF1的垂直平分线上,
∴xB=-
| a+c |
| 2 |
又e=
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴xB=-
| 3 |
| 4 |
| ||
| 4 |
| ||
| 8 |
∴k1=
| yB |
| xB+a |
| ||
| 2 |
(III)直线BD过定点(a,0),证明如下:
设P(a,0),B(xB,yB),则
| ||
| a2 |
| ||
| b2 |
则kAD•kPB=
| a2 |
| b2 |
| a2 |
| b2 |
| yB |
| xB+a |
| yB |
| xB-a |
| a2 |
| b2 |
| ||
|
| a2 |
| b2 |
| b2 |
| a2 |
∴PB⊥AD,又PD⊥AD,
∴三点P,B,D共线,即直线BD过定点P(a,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
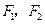 分别是双曲线
分别是双曲线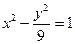 的左、右焦点.若点
的左、右焦点.若点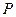 在双曲线上,且
在双曲线上,且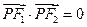 ,则
,则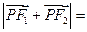 .
.