题目内容

已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）经过点A（1，
2
2
），且离心率为
2
2
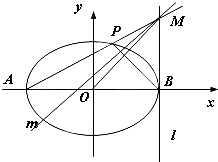
，过点B（2，0）的直线l与椭圆交于不同的两点M、N．
（Ⅰ）求椭圆的方程；
（Ⅱ）求
.
BM
•
.
BN
的取值范围．
（Ⅰ）由椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）经过点A（1，
2
2
），且离心率为
2
2
，
可得
e=
c
a
=
2
2
1
a2
+
1
2b2
=1
a2=b2+c2
，解得
a2=2
b=c=1
．
∴椭圆的方程为
x2
2
+y2=1．
（Ⅱ）由题意可知直线l的斜率存在，设其方程为y=k（x-2）．
设M（x1，y1），N（x2，y2）．由
y=k(x-2)
x2
2
+y2=1
得（1+2k2）x2-8k2x+8k2-2=0．
△=64k4-4（1+2k2）（8k2-2）＞0，得0≤k2＜
1
2
．
∴x1+x2=
8k2
1+2k2
，x1x2=
8k2-2
1+2k2
．
∵
BM
=(x1-2，y1)，
BN
=(x2-2，y2)，
∴
BM
•
BN
=（x1-2）（x2-2）+y1y2=（1+k2）（x1-2）（x2-2）=（1+k2）[x1x2-2（x1+x2）+4]=(1+k2)
2
1+2k2
=1+
1
1+2k2
，
∵0≤k2＜
1
2
，∴
3
2
＜1+
1
2k2
≤2，
∴
.
BM
•
.
BN
的取值范围是(
3
2
，2]．
练习册系列答案
相关题目
如图,椭圆中心在坐标原点,F为左焦点,当时,其离心率为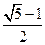,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于  ▲     
直线y=x+2与双曲线
x2
m
-
y2
3
=1有两个公共点，则m的取值范围是（　　）
A．m＞-1且m≠3B．0＜m＜7且m≠3C．m＞7D．m＜0
如图，在平面直角坐标系xOy中，椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的焦距为2，且过点(
2
，
6
2
)．
（1）求椭圆E的方程；
（2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M．
（ⅰ）设直线OM的斜率为k1，直线BP的斜率为k2，求证：k1k2为定值；
（ⅱ）设过点M垂直于PB的直线为m．求证：直线m过定点，并求出定点的坐标．
设椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)过点（1，
3
2
），F1，F2分别为椭圆C的左右焦点，且离心率e=
1
2

（1）求椭圆C的方程．
（2）已知A为椭圆C的左顶点，直线l过右焦点F2与椭圆C交于M，N两点，若AM、AN的斜率k1，k2满足k1+k2=-
1
2
，求直线l的方程．
如图，已知圆G：x2+y2-2x-
2
y=0，经过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F及上顶点B，过圆外一点（m，0）（m＞a）倾斜角为
5π
6
的直线l交椭圆于C，D两点，
（1）求椭圆的方程；
（2）若右焦点F在以线段CD为直径的圆E的内部，求m的取值范围．
如图，已知椭圆E1方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，圆E2方程为x2+y2=a2，过椭圆的左顶点A作斜率为k1直线l1与椭圆E1和圆E2分别相交于B、C．
（Ⅰ）若k1=1时，B恰好为线段AC的中点，试求椭圆E1的离心率e；
（Ⅱ）若椭圆E1的离心率e=
1
2
，F2为椭圆的右焦点，当|BA|+|BF2|=2a时，求k1的值；
（Ⅲ）设D为圆E2上不同于A的一点，直线AD的斜率为k2，当
k1
k2
=
b2
a2
时，试问直线BD是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．
已知椭圆C与双曲线
x2
2
-
y2
6
=1有相同焦点F1和F2，过F1的直线交椭圆于A、B两点，△ABF2的周长为8
3
．若直线y=t（t＞0）与椭圆C交于不同的两点E、F，以线段EF为直径作圆M．
（1）求椭圆C的标准方程；
（2）若圆M与x轴相切，求圆M被直线x-
3
y+1=0截得的线段长．
已知点P（-1，
3
2
）是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，F1、F2分别是椭圆C的左、右焦点，O是坐标原点，PF1⊥x轴．
①求椭圆C的方程；
②设A、B是椭圆C上两个动点，满足
PA
+
PB
=λ
PO
（0＜λ＜4，且λ≠2）求直线AB的斜率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网