题目内容
在△ABC中,角A,B,C的对边分别为 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若 ,
, ,求△ABC的面积;
,求△ABC的面积;
(2)若 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
(1)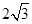 (2)△ABC为等边三角形。
(2)△ABC为等边三角形。
解析试题分析:(1)先由A,B,C成等差数列,解得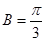 ,然后根据正弦定理得到
,然后根据正弦定理得到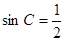 ,再利用面积公式即可;(2)由
,再利用面积公式即可;(2)由 ,
, ,
,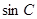 成等比数列,根据正弦定理得
成等比数列,根据正弦定理得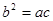 。
。
由余弦定理得
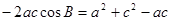 m联立得
m联立得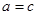 .
.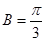 ,故可判断△ABC的形状.
,故可判断△ABC的形状.
试题解析:因为A,B,C成等差数列,所以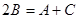 。
。
又A+B+C= ,所以
,所以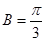 。
。
(1)解法一:因为 ,
, ,所以
,所以
由正弦定理得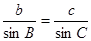 ,即
,即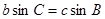 ,即
,即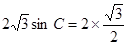 ,得
,得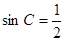 。 因为
。 因为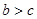 ,所以
,所以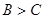 ,即C为锐角,所以
,即C为锐角,所以 ,从而
,从而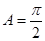 。
。
所以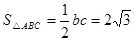 。
。
解法二:由余弦定理得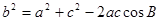 ,
,
即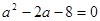 ,得
,得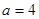 。
。
所以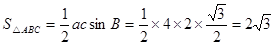 。
。
(2)因为 ,
, ,
,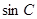 成等比数列,所以
成等比数列,所以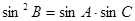 。
。
由正弦定理得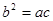 。由余弦定理得
。由余弦定理得
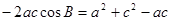 。
。
所以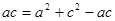 ,即
,即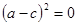 ,即
,即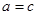 。:Zxxk.Com]
。:Zxxk.Com]
又因为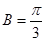 ,所以△ABC为等边三角形。
,所以△ABC为等边三角形。
考点:等差数列、等比数列的基本性质; 正弦定理; 余弦定理; 三角形面积公式.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知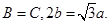
 的值;(2)
的值;(2) 的值.
的值.
 。
。
 (x≥0),
(x≥0), ,求用
,求用 表示
表示 的函数关系式,并求函数的定义域;
的函数关系式,并求函数的定义域; 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,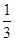 ,求B.
,求B. 的内角
的内角 所对边的长分别是
所对边的长分别是 ,且
,且
 的值;
的值; 的值.
的值.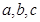 分别为
分别为 三个内角
三个内角 的对边,且
的对边,且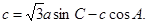
 ;
; ,△ABC的面积为
,△ABC的面积为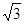 ,求
,求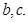
 内角
内角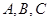 所对边长分别为
所对边长分别为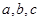 ,面积
,面积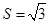 ,且
,且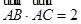 .
.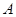 ;
;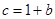 ,求
,求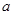 的值.
的值.