题目内容
△ABC的内角A,B,C的对边分别是a,b,c,已知3acosC=2ccosA,tanA=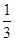 ,求B.
,求B.
135 .
.
解析试题分析:首先利用正弦定理把边用角的函数表示出来,然后利用同角三角函数的基本关系式求出tanA,tanC的值,最后再利用诱导公式和两角和的正切公式求解即可.
试题解析:由题设和正弦定理得,3sinAcosC=2sinCcosA,所以3tanAcosC=2sinC.因为tanA=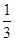 ,所以cosC=2sinC.
,所以cosC=2sinC.
tanC=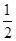 .所以tanB=tan[180
.所以tanB=tan[180 -(A+C)]=-tan(a+c)=
-(A+C)]=-tan(a+c)= =-1,即B=135
=-1,即B=135 .
.
考点:1. 正弦定理;2. 诱导公式和两角和与差的正切公式;3. 同角三角函数的基本关系式.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
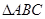 中,角
中,角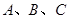 所对的边为
所对的边为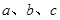 ,且满足
,且满足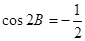 ,
,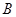 的值;(2)若
的值;(2)若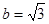 且
且 ,求
,求 的取值范围.
的取值范围. 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且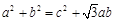 .
.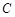 的值;(2)若
的值;(2)若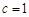 ,求
,求 的取值范围.
的取值范围. ≥0对一切实数
≥0对一切实数 恒成立.
恒成立. ,且A,B,C成等差数列。
,且A,B,C成等差数列。 ,
, ,求△ABC的面积;
,求△ABC的面积; 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。 中,
中, 是三个内角
是三个内角 的对边,关于
的对边,关于 的不等式
的不等式
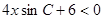 的解集是空集.
的解集是空集. 的最大值;
的最大值; ,
, ,求当角
,求当角 的值.[
的值.[ 的内角
的内角 所对边的长分别是
所对边的长分别是 ,且
,且 ,
, ,求
,求 与
与 的值.
的值. ,若
,若 .
. ,求
,求 的单调递增区间.
的单调递增区间.