题目内容
19.已知函数f(x)=2cosx(sinx+cosx),则下列说法正确的是( )| A. | f(x)的最小正周期为2π | |
| B. | f(x)的图象关于点$(-\frac{π}{8},0)$对称 | |
| C. | f(x)的图象关于直线$x=\frac{π}{8}$对称 | |
| D. | f(x)的图象向左平移$\frac{π}{4}$个单位长度后得到一个偶函数图象 |
分析 利用二倍角公式化简可得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,由正弦函数的图象和性质逐选项判断即可.
解答 解:∵f(x)=2cosx(sinx+cosx)=2sinxcosx+2cos2x=sin2x+1+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,
∴f(x)的最小正周期为$\frac{2π}{2}=π$,A错误;
由f(-$\frac{π}{8}$)=$\sqrt{2}$sin0+1=1,B错误;
由f($\frac{π}{8}$)=$\sqrt{2}$sin$\frac{π}{2}$+1=$\sqrt{2}+$1,C正确;
f(x)的图象向左平移$\frac{π}{4}$个单位长度后得到y=$\sqrt{2}$cos(2x+$\frac{π}{4}$)+1,不为偶函数,故D错误.
故选:C.
点评 本题主要考查了二倍角公式,正弦函数的图象和性质的应用,属于基础题.

练习册系列答案
相关题目
9.已知sinα+cosα=$\frac{1}{2}$,α∈(0,π),则$\frac{1-tanα}{1+tanα}$=( )
| A. | $\sqrt{7}$ | B. | -$\sqrt{7}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
7.下列四个集合:①A={x∈R|y=x2+1};②B={y|y=x2+1,x∈R};③C={(x,y)|y=x2+1,x∈R};④D={x|x≥1}.其中相同的集合是( )
| A. | ①与② | B. | ①与④ | C. | ②与③ | D. | ②与④ |
9.某人要制作一个三角形,要求它的三边的长度分别为3,4,6,则此人( )
| A. | 不能作出这样的三角形 | B. | 能作出一个锐角三角形 | ||
| C. | 能作出一个直角三角形 | D. | 能作出一个钝角三角形 |
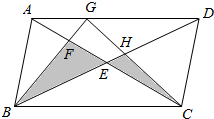 如图,长方形ABCD的面积为96cm2,四边形EFGH的面积为7.5cm2,那么阴影部分的面积是多少?
如图,长方形ABCD的面积为96cm2,四边形EFGH的面积为7.5cm2,那么阴影部分的面积是多少?