题目内容
14．等差数列{an}的公差d≠0，a1=20，且a3，a7，a9成等比数列．Sn为{an}的前n项和，则S10的值为110．分析 根据等比数列的性质建立条件关系，求出等差数列的公差，即可得到结论．
解答 解：由a3，a7，a9成等比数列，则a3a9=（a7）2，
即（a1+2d）（a1+8d）=（a1+6d）2，化简可得2a1d+20d2=0，
由a1=20，d≠0，解得d=-2．
则S10=10a1+$\frac{10×9}{2}$×（-2）=110，
故答案为：110．
点评 本题主要考查等差数列的性质和等差数列的求和，根据等比数列的性质求出等差数列的公差是解决本题的关键，属于基础题．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
如图，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2．过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2．
19．已知函数f（x）=2cosx（sinx+cosx），则下列说法正确的是（ ）
| A． | f（x）的最小正周期为2π | |
| B． | f（x）的图象关于点$（-\frac{π}{8}，0）$对称 | |
| C． | f（x）的图象关于直线$x=\frac{π}{8}$对称 | |
| D． | f（x）的图象向左平移$\frac{π}{4}$个单位长度后得到一个偶函数图象 |
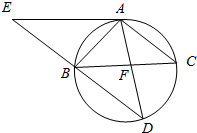如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=6，BD=5．
3．已知函数f（x）=ax2-2ax+c满足f（2013）＜f（-2012），则满足f（m）≤f（0）的实数m的取值范围是（ ）
| A． | （-∞，0] | B． | [2，+∞） | C． | （-∞，0]∪[2，+∞） | D． | [0，2] |
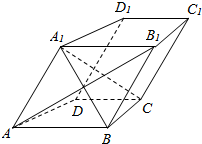如图，在四棱柱ABCD-A1B1C1D1中，AB∥C1D1，AB1⊥BC，且AA1=AB．