题目内容
18.极坐标方程(θ-$\frac{π}{4}$)ρ+(θ-$\frac{π}{4}$)sinθ=0的图形是直线y=x或圆${x}^{2}+(y+\frac{1}{2})^{2}=\frac{1}{4}$.分析 极坐标方程(θ-$\frac{π}{4}$)ρ+(θ-$\frac{π}{4}$)sinθ=0化为$θ=\frac{π}{4}$或ρ=-sinθ.$θ=\frac{π}{4}$表示经过原点且倾斜角为$\frac{π}{4}$的直线;ρ=-sinθ化为ρ2=-ρsinθ,化为直角坐标方程:x2+y2=-y.
解答 解:极坐标方程(θ-$\frac{π}{4}$)ρ+(θ-$\frac{π}{4}$)sinθ=0化为$θ=\frac{π}{4}$或ρ=-sinθ.
$θ=\frac{π}{4}$表示经过原点且倾斜角为$\frac{π}{4}$的直线,即y=x;
ρ=-sinθ化为ρ2=-ρsinθ,化为直角坐标方程:x2+y2=-y,即${x}^{2}+(y+\frac{1}{2})^{2}=\frac{1}{4}$,表示以$(0,-\frac{1}{2})$为圆心,$\frac{1}{2}$为半径的圆.
故答案为:直线y=x或${x}^{2}+(y+\frac{1}{2})^{2}=\frac{1}{4}$.
点评 本题考查了极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.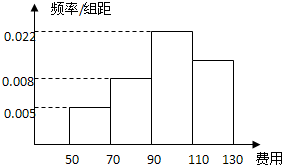 学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
 学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )| A. | 100 | B. | 120 | C. | 30 | D. | 300 |
7.若等差数列{an}前n项和Sn=n2+λ,则λ=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 任意实数 |