题目内容
13.证明:若a,b>0,则 lg$\frac{a+b}{2}$≥$\frac{lga+lgb}{2}$.分析 根据基本不等式、对数的运算性质和对数函数的性质进行证明即可.
解答 证明:∵当a,b>0时,$\frac{a+b}{2}≥\sqrt{ab}$,
∴两边取对数得$lg\frac{a+b}{2}≥lg\sqrt{ab}$,
又$lg\sqrt{ab}=\frac{lgab}{2}=\frac{lga+lgb}{2}$,
∴当a,b>0,$lg\frac{a+b}{2}≥\frac{lga+lgb}{2}$…(12分)
点评 本题考查对数的运算性质和对数函数的性质,以及基本不等式,属于基础题.

练习册系列答案
相关题目
2.已知函数f(x)=m•9x-3x,若存在非零实数x0,使得f(-x0)=f(x0)成立,则实数m的取值范围是( )
| A. | m≥$\frac{1}{2}$ | B. | m≥2 | C. | 0<m<2 | D. | 0<m<$\frac{1}{2}$ |
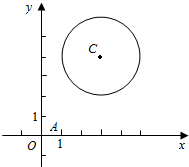 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).