题目内容
3．已知数列{an}的各项均为正数，Sn为数列{an}的前n项的和，且2Sn=${a}_{n}^{2}$+an，则数列{an}的首项a1=1；其通项公式an=n．分析 通过2Sn=${a}_{n}^{2}$+an与2Sn+1=${{a}_{n+1}}^{2}$+an+1作差、整理得an+1+an=（an+1+an）（an+1-an），进而可知数列{an}是以首项、公差均为1的等差数列，计算即得结论．
解答 解：∵2Sn=${a}_{n}^{2}$+an，
∴2Sn+1=${{a}_{n+1}}^{2}$+an+1，
两式相减得：2an+1=${{a}_{n+1}}^{2}$-${a}_{n}^{2}$+（an+1-an），
整理得：an+1+an=${{a}_{n+1}}^{2}$-${a}_{n}^{2}$=（an+1+an）（an+1-an），
又∵an+1+an≠0，
∴an+1-an=1，
又∵2a1=${{a}_{1}}^{2}$+a1，
解得：a1=1或a1=0（舍），
∴数列{an}是以首项、公差均为1的等差数列，
∴an=n，
故答案为：1，n．
点评 本题考查数列的通项，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
13．
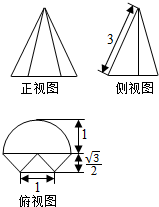一个几何体的三视图如图所示，其俯视图为一个半圆和一个等腰梯形，则该几何体的体积为（ ）
一个几何体的三视图如图所示，其俯视图为一个半圆和一个等腰梯形，则该几何体的体积为（ ）| A． | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | B． | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ | C． | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | D． | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ |