题目内容
15.已知平面直角坐标系xOy中,动点M到定点A(1,0),B(4,0)的距离之比为$\frac{1}{2}$,设动点M的轨迹为曲线C.(Ⅰ)求曲线C的方程;
(Ⅱ)过点B作斜率为0的直线l与曲线C相交于P,Q两点;
(ⅰ)若OP⊥OQ,求直线l的方程;
(ⅱ)求三角形APQ面积的最大值.
分析 (Ⅰ)利用直接法求曲线C的方程;
(Ⅱ)(ⅰ)设直线方程,若OP⊥OQ,则△POQ为等腰直角三角形,O到直线l的距离为$\sqrt{2}$,求出k,即可求直线l的方程;
(ⅱ)表示出三角形APQ面积,换元,利用配方法求出最大值.
解答 解:(Ⅰ)设M(x,y),则
∵动点M到定点A(1,0),B(4,0)的距离之比为$\frac{1}{2}$,
∴$\frac{\sqrt{(x-1)^{2}+{y}^{2}}}{\sqrt{(x-4)^{2}+{y}^{2}}}$=$\frac{1}{2}$,
化简可得x2+y2=4,
即曲线C的方程为x2+y2=4;
(Ⅱ)设直线l的方程为y=k(x-4)(k≠0),即kx-y-4k=0,
∵直线l与圆C相交,∴O到直线l的距离d=$\frac{4|k|}{\sqrt{1+{k}^{2}}}$<2,∴0<k2<$\frac{1}{3}$.
(ⅰ)若OP⊥OQ,则△POQ为等腰直角三角形,
∵|OP|=|OQ|=2,
∴O到直线l的距离为$\sqrt{2}$,
∴d=$\frac{4|k|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,
∴k=±$\frac{\sqrt{7}}{7}$,
∴直线l的方程为y=±$\frac{\sqrt{7}}{7}$(x-4);
(ⅱ)|PQ|=2$\sqrt{4-{d}^{2}}$=4$\sqrt{\frac{1-3{k}^{2}}{1+{k}^{2}}}$,
A到直线l的距离为$\frac{3|k|}{\sqrt{1+{k}^{2}}}$
∴三角形APQ面积S=$\frac{1}{2}$×4$\sqrt{\frac{1-3{k}^{2}}{1+{k}^{2}}}$×$\frac{3|k|}{\sqrt{1+{k}^{2}}}$,
设t=1+k2(1<t<$\frac{4}{3}$),S=6$\sqrt{\frac{(t-1)(4-3t)}{{t}^{2}}}$-6$\sqrt{-4(\frac{1}{t}-\frac{7}{8})^{2}+\frac{1}{16}}$,
∵$\frac{3}{4}$<$\frac{1}{t}$<1,
∴$\frac{1}{t}$=$\frac{7}{8}$,即k=±$\frac{\sqrt{7}}{7}$时,三角形APQ面积的最大值为$\frac{3}{2}$.
点评 本题考查轨迹方程,考查三角形面积的计算,考查点到直线距离公式的运用,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
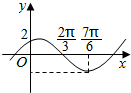 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一部分图象如图所示.