题目内容
(本小题满分12分)已知抛物线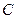 :
: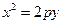 (
(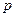 为正常数)的焦点为
为正常数)的焦点为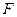 ,过
,过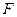 做一直线
做一直线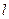 交抛物线
交抛物线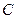 于
于
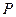 ,
,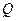 两点,点
两点,点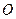 为坐标原点.
为坐标原点.
(1)若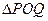 的面积记为
的面积记为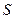 ,求
,求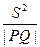 的值;
的值;
(2)若直线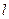 垂直于
垂直于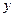 轴,过点P做关于直线
轴,过点P做关于直线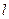 对称的两条直线
对称的两条直线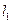 ,
,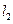 分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.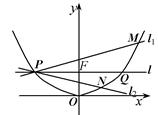
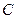 :
: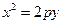 (
(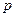 为正常数)的焦点为
为正常数)的焦点为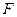 ,过
,过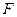 做一直线
做一直线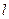 交抛物线
交抛物线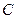 于
于
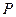 ,
,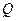 两点,点
两点,点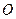 为坐标原点.
为坐标原点.(1)若
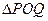 的面积记为
的面积记为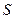 ,求
,求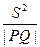 的值;
的值;(2)若直线
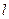 垂直于
垂直于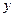 轴,过点P做关于直线
轴,过点P做关于直线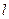 对称的两条直线
对称的两条直线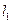 ,
, 分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
(1)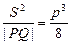 (2)略
(2)略
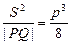 (2)略
(2)略(1)显然直线 斜率存在,
斜率存在,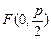 设
设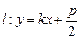 代入
代入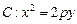 得
得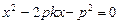 ,
,
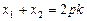 ,
,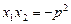 , ……2分
, ……2分
求得弦长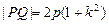 ,原点到直线
,原点到直线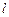 距离
距离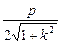 , ……2分
, ……2分
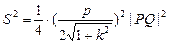 ,所以
,所以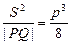 ……2分
……2分
(2)不妨设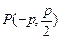 ,
,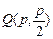 ,设
,设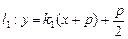 代入
代入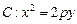 得
得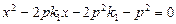 ,
,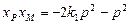 ,所以
,所以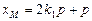 ,同理
,同理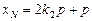 ,……2分
,……2分
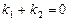 ,
,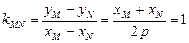 ,……2分
,……2分
抛物线在点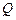 处的切线斜率
处的切线斜率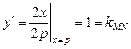 ,得证……2分
,得证……2分
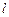 斜率存在,
斜率存在,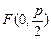 设
设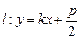 代入
代入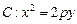 得
得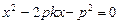 ,
,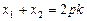 ,
,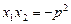 , ……2分
, ……2分求得弦长
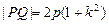 ,原点到直线
,原点到直线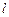 距离
距离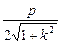 , ……2分
, ……2分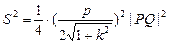 ,所以
,所以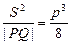 ……2分
……2分(2)不妨设
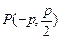 ,
,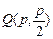 ,设
,设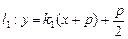 代入
代入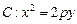 得
得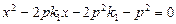 ,
,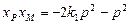 ,所以
,所以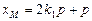 ,同理
,同理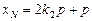 ,……2分
,……2分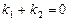 ,
,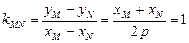 ,……2分
,……2分抛物线在点
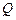 处的切线斜率
处的切线斜率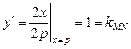 ,得证……2分
,得证……2分
练习册系列答案
相关题目
 :“方程
:“方程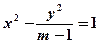 表示焦点在
表示焦点在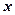 轴上的双曲线”,命题
轴上的双曲线”,命题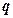 :“在区间
:“在区间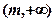 上,函数
上,函数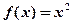 单调递增”,若
单调递增”,若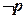 是真命题,
是真命题,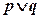 是真命题,求实数
是真命题,求实数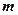 的取值范围。
的取值范围。 的两焦点
的两焦点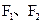 和短轴的两端点
和短轴的两端点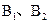 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为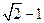 .
.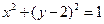 的任一条直径,求
的任一条直径,求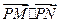 的最大值.
的最大值.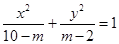 ,长轴在
,长轴在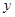 轴上. 若焦距为
轴上. 若焦距为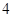 ,则
,则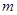 等于( )
等于( )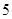 .
.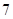 .
.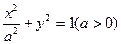 与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。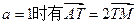 ,求点T坐标;
,求点T坐标;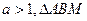 的面积为2,当
的面积为2,当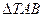 的面积的最大值为
的面积的最大值为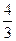 时,求曲线C的离心率e的取值范围。
时,求曲线C的离心率e的取值范围。 是圆
是圆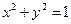 上的一个动点,过点
上的一个动点,过点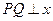 轴于点
轴于点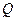 ,设
,设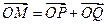 ,则点
,则点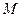 的轨迹方程______________;
的轨迹方程______________; 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 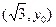 在该双曲线上,则
在该双曲线上,则 =( )
=( )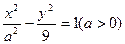 的一条渐近线方程为
的一条渐近线方程为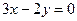 ,则
,则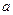 的值为 。
的值为 。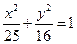 的焦点为
的焦点为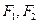 ,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 。
,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 。