题目内容
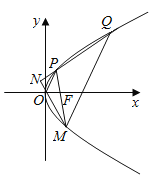
【题目】已知椭圆
的左、右顶点分别为A，B，点P在椭圆O上运动，若△PAB面积的最大值为
，椭圆O的离心率为
．
(1)求椭圆O的标准方程；
(2)过B点作圆E：
的两条切线，分别与椭圆O交于两点C，D(异于点B)，当r变化时，直线CD是否恒过某定点?若是，求出该定点坐标，若不是，请说明理由.
【答案】（1）
（2）直线
恒过定点
.
【解析】
（1）根据已知条件列方程组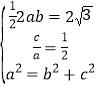
，解方程组可得.
（2）设过B的切线方程
，由d=r，利用韦达定理得两切线PC、PD的斜率
、
关系，把直线
、
代入椭圆方程求出C、D点坐标，利用两点式建立CD方程，化简方程可得.
（1）由题可知当点
在椭圆
的上顶点时，
最大，此时
，
所以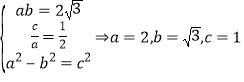
，
所以椭圆的标准方程为：.
（2）设过点
与圆
相切的直线方程为：
，即：
，
因为直线与圆：
相切，所以
，
即得
.
设两切线的斜率分别为
，则
，
设
，
，
由
，
∴
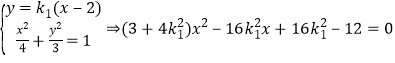，即
，∴
；
同理：
，
；
∴
，
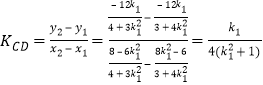所以直线的方程为：
.
整理得：
，
所以直线恒过定点
.
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
