题目内容
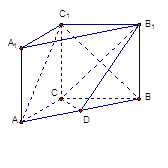
如图,在直三棱柱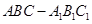 中,
中, 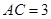 ,
, 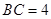 ,
,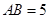 ,点
,点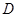 是
是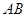 的中点.四面体
的中点.四面体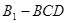 的体积是
的体积是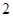 ,求异面直线
,求异面直线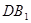 与
与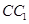 所成的角.
所成的角.
 中,
中, 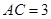 ,
, 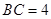 ,
,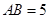 ,点
,点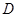 是
是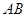 的中点.四面体
的中点.四面体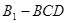 的体积是
的体积是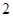 ,求异面直线
,求异面直线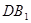 与
与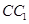 所成的角.
所成的角.
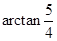
试题分析:因为
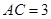 ,
, 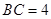 ,
,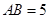 ,所以三角形ABC是直角三角形.又由直三棱柱
,所以三角形ABC是直角三角形.又由直三棱柱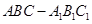 ,四面体
,四面体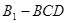 的体积是
的体积是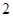 .所以可解得
.所以可解得 .又异面直线
.又异面直线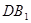 与
与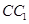 所成的角即
所成的角即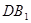 与
与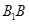 所成的角.即可解得.
所成的角.即可解得.试题解析:直三棱柱
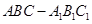 中
中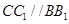
所以
 为异面直线
为异面直线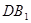 与
与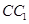 所成的角(或其补角) 3分
所成的角(或其补角) 3分直三棱柱
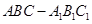 中
中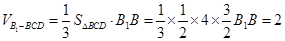 得
得 7分
7分
由点
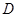 是
是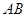 的中点得
的中点得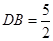
直三棱柱
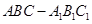 中
中
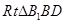 中
中
所以
 (或
(或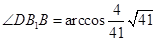 )
)所以异面直线
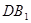 与
与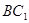 所成的角为
所成的角为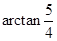 (或
(或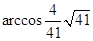 ) 12分
) 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 -A BC中,AB
-A BC中,AB  AC, AB=AC=2,
AC, AB=AC=2, =4,点D是BC的中点.
=4,点D是BC的中点. 与
与 所成角的余弦值;
所成角的余弦值; 与
与 所成二面角的正弦值.
所成二面角的正弦值.
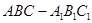 中,
中,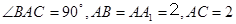 ,
,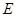 为
为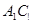 中点,求直线
中点,求直线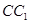 与平面
与平面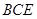 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)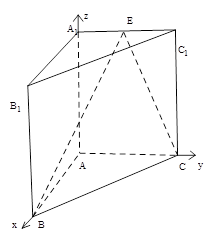
 中,AB=BC=2,
中,AB=BC=2,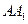 ,则
,则 与平面
与平面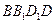 所成角的正弦值为( )
所成角的正弦值为( )



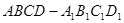 中,
中, ,则异面直线
,则异面直线 所成角的余弦值为( )
所成角的余弦值为( )



 中,
中, 与
与 、
、 所成角均为
所成角均为 ,
, ,且
,且 ,则
,则 与
与 所成角的余弦值为( )
所成角的余弦值为( )