题目内容
【题目】已知直线l:(k﹣1)x﹣2y+5﹣3k=0(k∈R)恒过定点P,圆C经过点A(4,0)和点P,且圆心在直线x﹣2y+1=0上.
(1)求定点P的坐标;
(2)求圆C的方程;
(3)已知点P为圆C直径的一个端点,若另一个端点为点Q,问:在y轴上是否存在一点M(0,m),使得△PMQ为直角三角形,若存在,求出m的值,若不存在,请说明理由.
【答案】
(1)解:由(k﹣1)x﹣2y+5﹣3k=0得,k(x﹣3)﹣(x+2y﹣5)=0,
令 ![]() ,得
,得 ![]() ,即定点P的坐标为(3,1).
,即定点P的坐标为(3,1).
(2)解:设圆C的方程为x2+y2+Dx+Ey+F=0,
由条件得 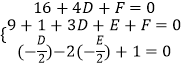 ,解得
,解得  .
.
所以圆C的方程为x2+y2﹣14x﹣8y+40=0,
圆C的标准方程(x﹣7)2+(y﹣4)2=25.
(3)解:圆C的标准方程为(x﹣7)2+(y﹣4)2=25,则 ![]() ,
,
设点P(3,1)关于圆心(7,4)的对称点为(x0,y0),则有 ![]() ,
,
解得x0=11,y0=7,故点Q的坐标为(11,7).
因为M在圆外,所以点M不能作为直角三角形的顶点,
若点P为直角三角形的顶点,则有 ![]() ,m=5,
,m=5,
若点Q是直角三角形的顶点,则有 ![]() ,
, ![]() ,
,
综上,m=5或 ![]() .
.
【解析】(1)左右直线l的方程:k(x﹣3)﹣(x+2y﹣5)=0,令 ![]() ,即可求得定点P的坐标;(2)设圆的方程,由题意列方程组,即可求圆的标准方程;(3)由(2)可知:求得直线CP的斜率,根据对称性求得Q点坐标,由M在圆外,所以点M不能作为直角三角形的顶点,分类讨论,即可求得m的值.
,即可求得定点P的坐标;(2)设圆的方程,由题意列方程组,即可求圆的标准方程;(3)由(2)可知:求得直线CP的斜率,根据对称性求得Q点坐标,由M在圆外,所以点M不能作为直角三角形的顶点,分类讨论,即可求得m的值.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
[85,95) | ① | 0.025 |
[95,105) | 0.050 | |
[105,115) | 0.200 | |
[115,125) | 12 | 0.300 |
[125,135) | 0.275 | |
[135,145) | 4 | ② |
[145,155] | 0.050 | |
合计 | ③ |
(1)根据图表,①②③处的数值分别为、、;
(2)在所给的坐标系中画出[85,155]的频率分布直方图; 
(3)根据题中信息估计总体落在[125,155]中的概率.
