题目内容
【题目】已知圆C经过A(3,2)、B(1,6),且圆心在直线y=2x上. (Ⅰ)求圆C的方程.
(Ⅱ)若直线l经过点P(﹣1,3)与圆C相切,求直线l的方程.
【答案】解:(Ⅰ)∵圆心在直线y=2x上, 故可设圆心C(a,2a),半径为r.
则圆C的标准方程为(x﹣a)2+(y﹣2a)2=r2 .
∵圆C经过A(3,2)、B(1,6),
∴ 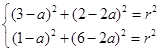 .
.
解得a=2,r= ![]() .
.
∴圆C的标准方程为
(x﹣2)2+(y﹣4)2=5.
(Ⅱ)由(Ⅰ)知,圆C的圆心为C(2,4),半径r= ![]() .
.
直线l经过点P(﹣1,3),
①若直线斜率不存在,
则直线l:x=﹣1.
圆心C(2,4)到直线l的距离为
d=3<r= ![]() ,故直线与圆相交,不符合题意.
,故直线与圆相交,不符合题意.
②若直线斜率存在,设斜率为k,
则直线l:y﹣3=k(x+1),
即kx﹣y+k+3=0.
圆心C(2,4)到直线l的距离为
d= ![]() =
= ![]() .
.
∵直线与圆相切,
∴d=r,即 ![]() =
= ![]() .
.
∴(3k﹣1)2=5+5k2 ,
解得k=2或k= ![]() .
.
∴直线l的方程为2x﹣y+5=0或x+2y﹣5=0
【解析】(Ⅰ)根据已知设出圆的标准方程,将点A,B的坐标代入标准方程,解方程组即可求出圆心及半径,从而得到圆C的方程. (Ⅱ)根据已知设出直线方程,利用直线与圆相切的性质d=r即可求出直线斜率k,从而求出直线方程.

练习册系列答案
相关题目
