题目内容
(本小题满分14分)已知圆 过点
过点
 , 且在
, 且在 轴上截得的弦
轴上截得的弦 的长为
的长为 .
.
(1) 求圆 的圆心的轨迹方程;
的圆心的轨迹方程;
(2) 若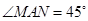 , 求圆
, 求圆 的方程.
的方程.
 过点
过点
 , 且在
, 且在 轴上截得的弦
轴上截得的弦 的长为
的长为 .
.(1) 求圆
 的圆心的轨迹方程;
的圆心的轨迹方程;(2) 若
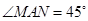 , 求圆
, 求圆 的方程.
的方程.(1)  ;(2)
;(2)
 ;(2)
;(2)
本题主要考查了利用圆的性质求解点的轨迹方程及圆的方程的求解,解题的关键是熟练 掌握圆的基本性质
(1)设圆C的圆心为C(x,y),圆的半径 r= x2+(y-a)2,由圆C在x轴上截得的弦MN的长为2a.可得|y|2+a2=r2,整理可求
(2)由∠MAN=45°可得∠MCN=90°,由(1)可知圆C的圆心为(x0,y0),则有x02=2ay0(结合y0="1" ,2|MN|=a可求x0,r,从而可求圆C的方程
解: (1)设圆 的圆心为
的圆心为 ,
,
依题意圆的半径 ……………… 2分
……………… 2分
∵ 圆 在
在 轴上截得的弦
轴上截得的弦 的长为
的长为 .
.
∴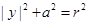
故 ………………………… 4分
………………………… 4分
∴
∴ 圆 的圆心的轨迹方程为
的圆心的轨迹方程为 ………………… 6分
………………… 6分
(2)∵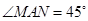 ,
,
∴ ……………………… 9分
……………………… 9分
令圆 的圆心为
的圆心为 , 则有
, 则有 (
( ) ,……… 10分
) ,……… 10分
又 ∵ …………………… 11分
…………………… 11分
∴ ……………………… 12分
……………………… 12分
∴ ……………………… 13分
……………………… 13分
∴ 圆 的方程为
的方程为  …………………14分
…………………14分
(1)设圆C的圆心为C(x,y),圆的半径 r= x2+(y-a)2,由圆C在x轴上截得的弦MN的长为2a.可得|y|2+a2=r2,整理可求
(2)由∠MAN=45°可得∠MCN=90°,由(1)可知圆C的圆心为(x0,y0),则有x02=2ay0(结合y0="1" ,2|MN|=a可求x0,r,从而可求圆C的方程
解: (1)设圆
 的圆心为
的圆心为 ,
, 依题意圆的半径
 ……………… 2分
……………… 2分∵ 圆
 在
在 轴上截得的弦
轴上截得的弦 的长为
的长为 .
.∴
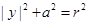
故
 ………………………… 4分
………………………… 4分∴

∴ 圆
 的圆心的轨迹方程为
的圆心的轨迹方程为 ………………… 6分
………………… 6分(2)∵
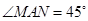 ,
, ∴
 ……………………… 9分
……………………… 9分令圆
 的圆心为
的圆心为 , 则有
, 则有 (
( ) ,……… 10分
) ,……… 10分又 ∵
 …………………… 11分
…………………… 11分∴
 ……………………… 12分
……………………… 12分∴
 ……………………… 13分
……………………… 13分∴ 圆
 的方程为
的方程为  …………………14分
…………………14分
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 上,与直线
上,与直线 相切,在
相切,在 上截得弦长为6,求该圆的方程.
上截得弦长为6,求该圆的方程. ,一条直径的两个端点分别在
,一条直径的两个端点分别在 轴和
轴和 轴上,则此圆的方
轴上,则此圆的方


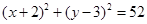

 的半径为2,则其圆心坐标为 。
的半径为2,则其圆心坐标为 。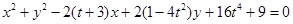 表示一个圆.
表示一个圆. 的取值范围
的取值范围  m),则sin2α=
m),则sin2α=
