题目内容
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过坐标原点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两点.是否存在常数
两点.是否存在常数![]() , 满足
, 满足![]() ?若存在,求出这个常数;若不存在,请说明理由.
?若存在,求出这个常数;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得 ,解得a2=12,b2=8,即可求出椭圆方程,
,解得a2=12,b2=8,即可求出椭圆方程,
(2)设出直线l的方程为x=my+2,代入椭圆方程,运用韦达定理和弦长公式,求出|AB|,再设直线x=my,代入椭圆方程,化简可得|OP|,再由计算即可得到所求常数λ.
(1)由题意可得 ,解得a2=12,b2=8,c2=4,
,解得a2=12,b2=8,c2=4,
故椭圆C的方程为![]() 1,
1,
(2)设直线AB的方程为x=my+2,A(x1,y1),B(x2,y2),
由
得(2m2+3)y2+8my﹣16=0,
即有y1+y2![]() ,y1y2
,y1y2![]() ,
,
|AB|![]()
![]()
![]() 8
8![]()
![]() ,
,
设P(x3,y3),Q(x4,y4),
由x=my代入椭圆方程可得
消去x,并整理得y2![]() ,
,
∴x2=m2![]() ,
,
∴|OP|2![]() ,
,
∵|AB|=λ|OP|2,
∴8![]()
![]() λ
λ![]() ,
,
∴λ![]()
故存在常数λ![]() ,使得|AB|=λ|OP|2
,使得|AB|=λ|OP|2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于![]() 的回归方程
的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数
恰好等于相关系数![]() 的平方,当
的平方,当![]() 时,认为线性回归模型是有效的,请计算
时,认为线性回归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到
并且评价模型的拟合效果(计算结果精确到![]() ).
).
附:
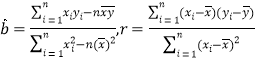 ,
, ![]() .
.