题目内容
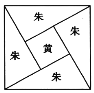
【题目】《周髀算经》中给出了勾股定理的绝妙证明.下图是赵爽弦图及注文，弦图是一个以勾股形之弦为边的正方形，其面积称为弦实，图中包含四个全等的勾股形及一个小正方形，分别涂成朱色及黄色，其面积称为朱实、黄实.由2
勾股
（股
勾）2
4朱实黄实弦实，化简得勾2股2弦2.若图中勾股形的勾股比为
，若向弦图内随机抛掷2000颗图钉（大小忽略不计），则落在黄色图形内的图钉颗数大约为（ ）（参考数据：
）
A.
B.
C.
D.
【答案】B
【解析】
先求得大正方形和小长方形的面积，然后利用几何概型对落在黄色图形内的图钉颗数进行估计.
由于图中勾股形的勾股比为
，不妨设为
和
，
故大正方形的边长为
，小正方形的边长为
.
所以大正方形的面积为
，小正方形的面积为
.
设落在黄色图形内的图钉颗数大约为
，
则
，
即
.
故选：B
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
