题目内容
【题目】关于函数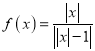 ,给出以下四个命题,其中真命题的序号是_______.
,给出以下四个命题,其中真命题的序号是_______.
①![]() 时,
时,![]() 单调递减且没有最值;
单调递减且没有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;
④![]() 是偶函数且有最小值.
是偶函数且有最小值.
【答案】②④
【解析】
①将函数![]() 表示为分段函数,结合分式型函数的单调性进行判断;②由函数
表示为分段函数,结合分式型函数的单调性进行判断;②由函数![]() 是偶函数,在
是偶函数,在![]() 且
且![]() 时,判定函数
时,判定函数![]() 与函数
与函数![]() 在
在![]() 时有唯一交点,同理得出,当
时有唯一交点,同理得出,当![]() 且
且![]() 时,函数
时,函数![]() 与函数
与函数![]() 在
在![]() 时有交点,从而可得方程
时有交点,从而可得方程![]() 有解;③求方程
有解;③求方程![]() 的解,即可判断出命题③的正误;④利用偶函数的定义判定函数
的解,即可判断出命题③的正误;④利用偶函数的定义判定函数![]() 为偶函数,再利用绝对值的性质得出
为偶函数,再利用绝对值的性质得出![]() 且
且![]() ,即可判断出命题④的正误.
,即可判断出命题④的正误.
对于命题①,当![]() 时,
时,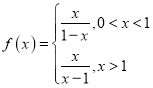 .
.
当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,此时,
上单调递增,此时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,
上单调递减,
所以,当![]() 时,函数
时,函数![]() 不单调且没有最值,命题①错误;
不单调且没有最值,命题①错误;
对于命题②,当![]() 时,
时,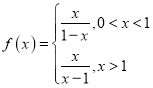 ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,构造函数
时,构造函数![]() ,
,
则函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以,函数![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
即当![]() 时,方程
时,方程![]() 在
在![]() 上有解.
上有解.
函数![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,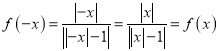 ,则函数
,则函数![]() 为偶函数,
为偶函数,
同理可知,当![]() 时,方程
时,方程![]() 在
在![]() 上有解.
上有解.
所以,命题②正确;
对于命题③,当![]() 时,令
时,令![]() ,解得
,解得![]() ,则命题③错误;
,则命题③错误;
对于命题④,由②可知,函数![]() 是偶函数,由绝对值的性质可知
是偶函数,由绝对值的性质可知![]() 且
且![]() ,则函数
,则函数![]() 为偶函数且最小值为
为偶函数且最小值为![]() ,命题④正确.
,命题④正确.
因此,正确命题的序号为②④.
故答案为:②④.

练习册系列答案
相关题目