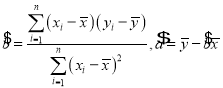题目内容
【题目】甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试与面试通过的概率分别为0.8,0.5,乙笔试与面试通过的概率分别为0.8,0.4,且笔试通过了才能进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响.
(1)求这两人至少有一人通过笔试的概率;
(2)求这两人笔试都通过却都未被录用的概率;
(3)记这两人中最终被录用的人数为X,求X的分布列和数学期望.
【答案】(1)0.96;(2)0.192;(3)分布列见解析,数学期望0.72
【解析】
(1)利用独立事件与对立事件的概率公式求解即可;(2)直接利用独立事件的概率公式求解即可;(3)X可取0,1,2, 利用独立事件与对立事件的概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
(1)设“这两人至少有一人通过笔试”为事件A,
则P(A)=1![]() P(
P(![]() )=1
)=1![]() (1
(1![]() 0.8)2=0.96.
0.8)2=0.96.
(2)设“这两人笔试都通过却都未被录用”为事件B,
则P(B)=0.82×(1![]() 0.5)×(1
0.5)×(1![]() 0.4)=0.192.
0.4)=0.192.
(3)甲、乙两人被录用的概率分别为0.8×0.5=0.4,0.8×0.4=0.32.
由题意可得X可取0,1,2,则
P(X=0)=(1![]() 0.4)×(1
0.4)×(1![]() 0.32)=0.408,
0.32)=0.408,
P(X=1)=(1![]() 0.4)×0.32+0.4×(1
0.4)×0.32+0.4×(1![]() 0.32)=0.464,
0.32)=0.464,
P(X=2)=0.4×0.32=0.128,
所以X的分布列为
X | 0 | 1 | 2 |
P | 0.408 | 0.464 | 0.128 |
故E(X)=0×0.408+1×0.464+2×0.128=0.72.

【题目】为了解某地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(已知:![]() 则认为
则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般,
线性相关性一般,![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y与x的线性回归方程,并预测该地区2019年足球特色学校的个数(精确到个位)
参考公式:
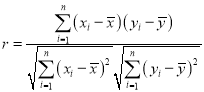
![]() ;
;