题目内容
2.某几何体的三视图如图所示,它的表面积为( )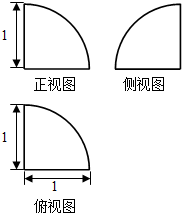
| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
分析 由已知中的三视图,可知该几何体是一个半径为1的$\frac{1}{8}$球,分别计算它的各个面的面积,相加可得答案.
解答 解:根据三视图,该几何体为$\frac{1}{8}$个球,半径为1.
∴它的表面积S=3×$\frac{1}{4}$×π•12+$\frac{1}{8}×4$×π•12=$\frac{5π}{4}$.
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
17.若集合A={2,0},B={1,5},则A∩B=( )
| A. | ∅ | B. | {0} | C. | {0,1} | D. | {2,0,1,5} |
14.设直线:l:y=kx+m(m≠0),双曲线C:$\frac{x^2}{16}-\frac{y^2}{9}$=1(a>0,b>0),则“k=±$\frac{3}{4}$”是“直线l与双曲线C恰有一个公共点“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
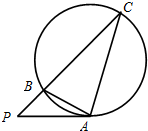 如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.
如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.