题目内容
2．已知a＞0，a≠1，命题p：y=loga（x+1）在（0，+∞）上单调递减，命题q：曲线y=x2+（2a-3）x+1与x轴交于不同的两点，若p∧q为假命题，p∨q为真命题，求实数a的取值范围．分析 先根据对数函数的单调性，和二次函数图象和x轴交点的情况与判别式的关系即可求出命题p，q下的a的取值范围．根据p∧q为假，p∨q为真即可判断p，q的真假情况，根据p，q的真假情况即可求出a的取值范围．
解答 解：p：∵函数y=loga（x+1）在（0，+∞）上单调递减；
∴0＜a＜1；
q：曲线y=x2+（2a-3）x+1与x轴交于不同的两点；
∴△=（2a-3）2-4＞0，解得a＜$\frac{1}{2}$，或a＞$\frac{5}{2}$；
∵p∧q为假，p∨q为真，
∴p，q一真一假；
若p真q假，则：0＜a＜1，且$\frac{1}{2}$≤a≤$\frac{5}{2}$，
∴$\frac{1}{2}$≤a＜1；
若p假q真，则：a＞1，且a＜$\frac{1}{2}$，或a＞$\frac{5}{2}$，
∴a＞$\frac{5}{2}$；
∴实数a的取值范围为[$\frac{1}{2}$，1）∪（$\frac{5}{2}$，+∞）．
点评 本题考查对数函数的单调性，二次函数图象和x轴交点的情况与判别式△的关系，p∧q，p∨q的真假和p，q真假的关系．
练习册系列答案
备战中考寒假系列答案
相关题目
2．某几何体的三视图如图所示，它的表面积为（ ）
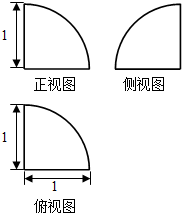
| A． | $\frac{π}{4}$ | B． | $\frac{5π}{4}$ | C． | $\frac{7π}{8}$ | D． | π |
3．已知点A的坐标为（4$\sqrt{3}$，1），将OA绕坐标原点O逆时针旋转$\frac{π}{3}$至OB，则点B的纵坐标为（ ）
| A． | $\frac{{3\sqrt{3}}}{2}$ | B． | $\frac{{5\sqrt{3}}}{2}$ | C． | $\frac{11}{2}$ | D． | $\frac{13}{2}$ |
10．定义运算“•”如下：x•y=$\left\{\begin{array}{l}{x，x≥y}\\{y，x＜y}\end{array}\right.$，若函数f（x）=m-（1-2x）•（2x-2）有两个零点，则（ ）
| A． | m∈（-$\frac{1}{2}$，+∞） | B． | m∈（-$\frac{1}{2}$，1） | C． | m∈[-$\frac{1}{2}$，+∞） | D． | m∈[-$\frac{1}{2}$，1） |
17．以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l的参数方程为$\left\{\begin{array}{l}x=3-t\\ y=t-5\end{array}\right.$（t为参数），圆C的极坐标方程为ρ=4（cosθ+sinθ），则圆C上的点到直线l的距离的最大值为（ ）
| A． | 2$\sqrt{2}$ | B． | 3$\sqrt{2}$ | C． | 4$\sqrt{2}$ | D． | 5$\sqrt{2}$ |
某中学为了解高三学生数学课程的学习情况，从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析，得到如下的样本的频率分布直方图，已知成绩在[80，90）的学生共有40人，则样本中成绩在[60，80）内的人数为（ ）