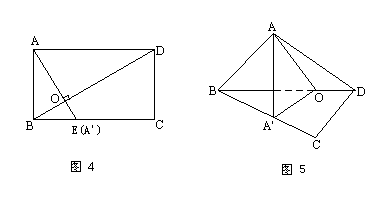
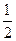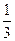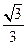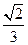题目内容
如图,△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=
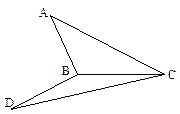 ∠DBC=120°,求
∠DBC=120°,求
(1) A、D连线和直线BC所成角的大小;
(2) 二面角A-BD-C的大小
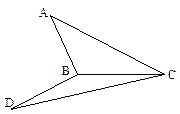 ∠DBC=120°,求
∠DBC=120°,求(1) A、D连线和直线BC所成角的大小;
(2) 二面角A-BD-C的大小
在平面ADC内作AH⊥BC,H是垂足,连HD.因为平面ABC⊥平面BDC.所以AH⊥平面BDC.HD是AD在平面BDC的射影.依题设条件可证得HD⊥BC,由三垂线定理得AD⊥BC,即异面直线AD和BC形成的角为90°.
在平面BDC内作HR⊥BD,R是垂足,连AR.HR是AR在平面BDC的射影,∴AR⊥BD,∠ARH是二面角A-BD-C的平面角的补角,设AB=a,可得,
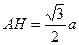 ,
,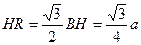 ,
,
∴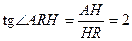 .
.
∴二面角A-BD-C的大小为π-arctg2.
在平面BDC内作HR⊥BD,R是垂足,连AR.HR是AR在平面BDC的射影,∴AR⊥BD,∠ARH是二面角A-BD-C的平面角的补角,设AB=a,可得,
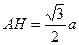 ,
,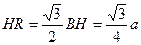 ,
,∴
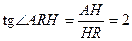 .
.∴二面角A-BD-C的大小为π-arctg2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
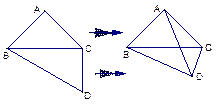
 中,侧面
中,侧面 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 平面
平面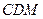 ;
; 的余弦值.
的余弦值.
 平面
平面 ,
, ,
, ,
, ,
, ,
, 的大小.
的大小.
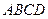 是
是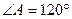 的菱形,绕AC将该菱形折成二面角
的菱形,绕AC将该菱形折成二面角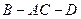 ,记异面直线
,记异面直线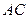 、
、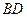 所成角为
所成角为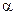 ,
,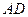 与平面
与平面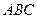 所成角为
所成角为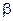 ,当
,当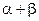 最大时,二面角
最大时,二面角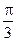
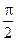
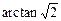
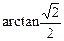
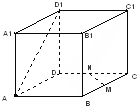
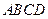 中,已知棱
中,已知棱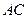 的长为
的长为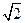 ,其余各棱长都为
,其余各棱长都为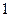 ,则二面角
,则二面角 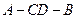 的余弦值为( )
的余弦值为( )