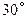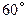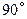题目内容
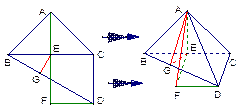
一副三角板拼成一个四边形ABCD，如图，然后将它沿BC折成直二面角.
(1)求证: 平面ABD⊥平面ACD；
(2)求AD与BC所成的角；
(3)求二面角A—BD—C的大小.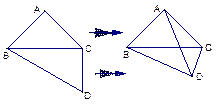
(1)求证: 平面ABD⊥平面ACD；
(2)求AD与BC所成的角；
(3)求二面角A—BD—C的大小.
(1)证明略 (2)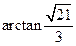
(3) 二面角A—BD—C的大小为arctan2
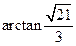(3) 二面角A—BD—C的大小为arctan2 取BC中点E，连结AE，∵AB=AC，∴AE⊥BC
∵平面ABC⊥平面BCD，∴AE⊥平面BCD，
∵BC⊥CD，由三垂线定理知AB⊥CD.
又∵AB⊥AC，∴AB⊥平面BCD，∵AB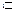
平面ABD.
∴平面ABD⊥平面ACD。
(2)解: 在面BCD内，过D作DF∥BC，过E作EF⊥DF，交DF于F，由三垂线定理知AF⊥DF，∠ADF为AD与BC所成的角.
设AB=m，则BC=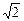
m，CE=DF=
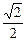m,CD=EF=
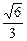m
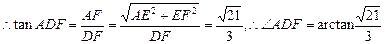
即AD与BC所成的角为arctan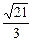
(3)解:∵AE⊥面BCD，过E作EG⊥BD于G，连结AG，由三垂线定理知AG⊥BD，
∴∠AGE为二面角A—BD—C的平面角
∵∠EBG=30°，BE=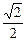m,∴EG=
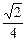m
又AE=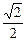m,∴tanAGE=
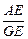=2,∴∠AGE=arctan2.
即二面角A—BD—C的大小为arctan2.
另法（向量法）: (略)
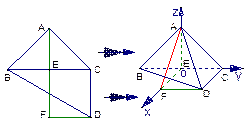
∵平面ABC⊥平面BCD，∴AE⊥平面BCD，
∵BC⊥CD，由三垂线定理知AB⊥CD.
又∵AB⊥AC，∴AB⊥平面BCD，∵AB
平面ABD. ∴平面ABD⊥平面ACD。
(2)解: 在面BCD内，过D作DF∥BC，过E作EF⊥DF，交DF于F，由三垂线定理知AF⊥DF，∠ADF为AD与BC所成的角.
设AB=m，则BC=
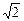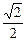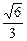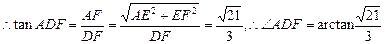
m，CE=DF=m,CD=EF=m即AD与BC所成的角为arctan
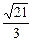
(3)解:∵AE⊥面BCD，过E作EG⊥BD于G，连结AG，由三垂线定理知AG⊥BD，
∴∠AGE为二面角A—BD—C的平面角
∵∠EBG=30°，BE=
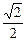m,∴EG=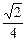m又AE=
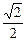m,∴tanAGE=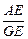=2,∴∠AGE=arctan2.即二面角A—BD—C的大小为arctan2.
另法（向量法）: (略)
练习册系列答案
初中学业考试导与练系列答案
相关题目
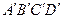的对角线
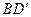上，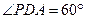
。
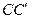所成角的大小；
所成角的大小。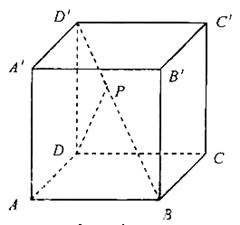
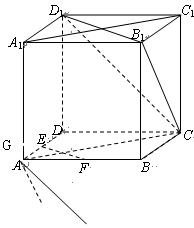
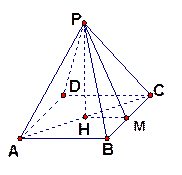
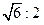，则其侧面与底面的夹角为( ). 
、
； 
、
； 
、
； 
、
.
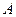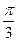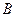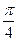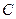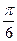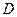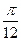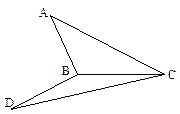∠DBC=120°，求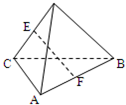
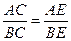．把这个结论类比到空间：在三棱锥A—BCD中（如下图），DEC平分二面角A—CD—B且与AB相交于E，则得到类比的结论是_________.
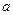和它在平面内的射影的夹角是
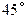，且平面内的直线
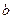和斜线
