题目内容
4.两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$所成的角是( )| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
分析 通过向量的模相等,判断三个向量的关系,然后求出$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$所成的角
解答 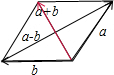 解:因为两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,根据其几何意义得到向量位置关系如图,
解:因为两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,根据其几何意义得到向量位置关系如图,
所以以两个向量为两边之差的四边形是菱形,两者的夹角为120°,所以$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$所成的角为30°;
故选:D.
点评 本题是基础题,考查向量加减法的意义,可以利用向量数量积求解向量的夹角,考查计算能力.

练习册系列答案
相关题目
15.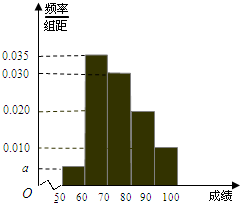 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均数.
 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均数.
9.在△ABC中,AB=3,AC=2,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则直线AD通过△ABC的( )
| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
10.下列说法正确的是( )
| A. | 有两个面平行,其余各面都是平行四边形的几何体是棱柱 | |
| B. | 用斜二测法画平行四边形的直观图一定是平行四边形 | |
| C. | 用一个面去截棱锥,底面和斜面之间的部分组成的几何体叫做棱台 | |
| D. | 平行与同一平面的两条直线平行 |