题目内容

19．把边长为1的正方形ABCD沿对角线BD折起，使得平面ABD⊥平面CBD，形成三棱锥C-ABD的正视图与俯视图如右图所示，则侧视图的面积为$\frac{1}{4}$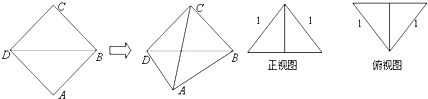

分析 根据三棱锥的正视图和俯视图确定三棱锥的侧视图，根据侧视图的结构计算面积即可．

解答 解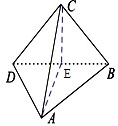：取BD的中点E，连结CE，AE，
∵平面ABD⊥平面CBD，
∴CE⊥AE，
∴三角形直角△CEA是三棱锥的侧视图，
∵BD=$\sqrt{2}$，∴CE=AE=$\frac{\sqrt{2}}{2}$，
∴△CEA的面积S=$\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．

点评 本题主要考查三视图的识别和应用，根据三棱锥的结构得到三棱锥的侧视图是解决本题的关键．

练习册系列答案
相关题目
9．已知h＞0，a，b∈R，甲：|a-b|＜2h，乙：|a-1|＜h且|b-1|＜h，则甲是乙的必要不充分条件．
10．设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2$\sqrt{2}$，求a的值；
（2）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=$\frac{\sqrt{2}}{2}$，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
7．复数$\frac{2}{1-i}-i$（i为虚数单位）等于1．
14．已知命题：①“所有能被3整除的整数都是奇数”的否定是“存在一个能被3整除的整数不是奇数”
②“菱形的两条对角线互相垂直”的逆命题；
③“a，b，c∈R，若a＞b，则a+c＞b+c”的逆否命题；
④“若a+b≠3，则a≠1或b≠2”．上述命题中真命题的个数为（　　）
A．1B．2C．3D．4
4．两个非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|，则$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$所成的角是（　　）
A．150°B．120°C．60°D．30°
11．点A（sin2015°，cos2015°）在平面直角坐标系平面上位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
8．已知向量$\overrightarrow{a}$=（5$\sqrt{3}$cosx，cosx），$\overrightarrow{b}$=（sinx，2cosx），设函数f（x）=$\overrightarrow{a}$$•\overrightarrow{b}$+|$\overrightarrow{b}$|2+$\frac{3}{2}$．
（Ⅰ）当x∈[0，$\frac{π}{2}$]时，求函数f（x）的最小值；
（Ⅱ）当x∈[$\frac{π}{6}$，$\frac{π}{2}$]时，若f（x）=8，求函数f（x+$\frac{π}{8}$）的值．
5．某程序框图如图所示，若该程序运行后输出的值是$\frac{5}{6}$，则（　　）
A．a=4B．a=5C．a=6D．a=7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网