题目内容
14.过点A(0,$\frac{7}{3}$)与点B(7,0)的直线l1与过点C(2,1)与点D(3,k+1)的直线l2与两坐标轴正半轴围成的四边形内接于一个圆,求实数k的值.(画图作答)分析 根据四点共圆的条件可知,四边形的2个对角之和是180°,即l1与l2是相互垂直的,利用两条直线斜率的乘积为-1,即可得到结论.
解答 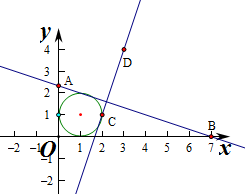 解:∵过点A﹙0,$\frac{7}{3}$﹚,B﹙7,0﹚的直线l1与过点C﹙2,1﹚,D﹙3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,
解:∵过点A﹙0,$\frac{7}{3}$﹚,B﹙7,0﹚的直线l1与过点C﹙2,1﹚,D﹙3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,
∴根据四点共圆的条件可知l1与l2是相互垂直,
即l1与l2对应的斜率满足k1•k2=-1,
即$\frac{\frac{7}{3}}{-7}•\frac{k+1-1}{3-2}$=-1,
解得k=3.
点评 本题主要考查直线垂直与直线斜率之间的关系,利用四点共圆得到直线垂直是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.点P(0,5)到直线2x+1=0的距离为( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
6.数列{an}的通项公式是an=$\frac{1}{n(n+1)}$(n∈N*),若前n项的和为$\frac{2014}{2015}$,则项数n为( )
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
 如图,在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30米至C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$米至D处,测得顶端A的仰角为4θ,则θ的值为15°.
如图,在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30米至C处测得顶端A的仰角为2θ,再继续前进10$\sqrt{3}$米至D处,测得顶端A的仰角为4θ,则θ的值为15°.