题目内容
9.在△ABC中,AB=3,AC=2,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则直线AD通过△ABC的( )| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
分析 计算出|$\frac{1}{2}$$\overrightarrow{AB}$|=|$\frac{3}{4}$$\overrightarrow{AC}$|=$\frac{3}{2}$,又因为$\overrightarrow{AD}$=$\frac{1}{2}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$,设$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{3}{4}$$\overrightarrow{AC}$,由向量加法的平行四边形法则可知四边形AEDF为菱形,从而可确定直线AD通过△ABC的内心.
解答 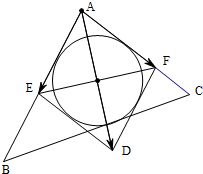 解:∵AB=3,AC=2
解:∵AB=3,AC=2
∴|$\frac{1}{2}$$\overrightarrow{AB}$|=$\frac{3}{2}$,|$\frac{3}{4}$$\overrightarrow{AC}$|=$\frac{3}{2}$.
即|$\frac{1}{2}$$\overrightarrow{AB}$|=|$\frac{3}{4}$$\overrightarrow{AC}$|=$\frac{3}{2}$
设$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{3}{4}$$\overrightarrow{AC}$,
则|$\overrightarrow{AE}$|=|$\overrightarrow{AF}$|,
∴$\overrightarrow{AD}$=$\frac{1}{2}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$=$\overrightarrow{AE}$+$\overrightarrow{AF}$.
由向量加法的平行四边形法则可知,四边形AEDF为菱形.
∴AD为菱形的对角线,
∴AD平分∠EAF.
∴直线AD通过△ABC的内心.
故选:C.
点评 本题考查三角形内心的判断,根据向量长度,结合向量加法的平行四边形法则及其几何意义是解决本题的关键.

| A. | $±\frac{\sqrt{3}}{3}$ | B. | $±\frac{\sqrt{3}}{2}$ | C. | ±1 | D. | $±\sqrt{3}$ |
| A. | 13 | B. | 19 | C. | 20 | D. | 51 |
| A. | y=x+2 | B. | y=-x+1 | C. | y=x-2 | D. | y=-x+4 |
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | (-1,-1) | D. | (-3,-2) |