题目内容
【题目】过![]() 轴上动点
轴上动点![]() 引抛物线
引抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,其中
,其中![]() ,
,![]() 为切线.
为切线.
(1)若切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,求证:
,求证:![]() 为定值,并求出定值;
为定值,并求出定值;
(2)当![]() 最小时,求
最小时,求![]() 的值.
的值.
【答案】(1)证明见解析,![]() 为定值-4(2)
为定值-4(2)![]()
【解析】
(1)联立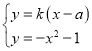 ,得
,得![]() ,则
,则![]() ,
,![]() 是方程
是方程![]() 的解,故
的解,故![]() ,即
,即![]() 为定值
为定值![]() .
.
(2)要使![]() 最小,就是使得
最小,就是使得![]() 到直线
到直线![]() 的距离最小,首先求出直线
的距离最小,首先求出直线![]() 的方程,利用点到直线公式和基本不等式得到:
的方程,利用点到直线公式和基本不等式得到:![]() 到直线
到直线![]() 的距离最小值时
的距离最小值时![]() ,再联立
,再联立![]() 得到
得到![]() ,
,![]() ,
,![]() ,带入
,带入![]() 即可.
即可.
(1)设过![]() 与抛物线
与抛物线![]() 相切的直线的斜率是
相切的直线的斜率是![]() ,
,
则该切线方程为:![]() .
.
由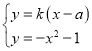 ,得
,得![]() .
.
∴![]() .
.
则![]() ,
,![]() 是方程
是方程![]() 的解,
的解,
故![]() ,即
,即![]() 为定值
为定值![]() .
.
(2)要使![]() 最小,就是使得
最小,就是使得![]() 到直线
到直线![]() 的距离最小.
的距离最小.
设![]() ,
,![]() ,由题知:
,由题知:
![]() ,
,![]() .
.
故切线![]() 的方程为:
的方程为:![]() .
.
则![]() ,
,
整理得:![]() .同理得:
.同理得:![]() .
.
所以![]() .
.
直线![]() 的方程为
的方程为![]() .
.
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则
![]()
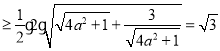
当且仅当![]() 即
即![]() 时取等号
时取等号
由![]() 得
得![]()
则![]() ,
,![]()
∴![]()
![]()
![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目