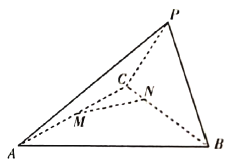
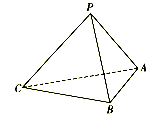
题目内容
【题目】某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有![]() 或者
或者![]() 两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为![]() ,记抽到的废品数为
,记抽到的废品数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
【答案】(1) 在不开箱检验的情况下,可以购买. (2) ①分布列见解析,0.4 ②不可以购买
【解析】
(1)求出在不开箱检验的情况下,一箱产品中正品的价格期望值,即得解;(2)①![]() 的可能取值为0,1,2,再求出对应的概率,即得
的可能取值为0,1,2,再求出对应的概率,即得![]() 的分布列和数学期望;②一箱产品中,设正品的价格的期望值为
的分布列和数学期望;②一箱产品中,设正品的价格的期望值为![]() ,求出
,求出![]() 即得解.
即得解.
(1)在不开箱检验的情况下,一箱产品中正品的价格期望值为:
![]() ,
,
∴在不开箱检验的情况下,可以购买.
(2)①![]() 的可能取值为0,1,2,
的可能取值为0,1,2,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
| 0.64 | 0.32 | 0.04 |
![]() .
.
②设事件![]() :发现在抽取检验的2件产品中,其中恰有一件是废品,
:发现在抽取检验的2件产品中,其中恰有一件是废品,
则![]() ,
,
一箱产品中,设正品的价格的期望值为![]() ,则
,则![]() ,
,
事件![]()
![]() 的一箱,
的一箱,
则![]() ,
,
事件![]() :抽取的废品率为
:抽取的废品率为![]() 的一箱,
的一箱,
则![]() ,
,
∴![]() ,
,
∴已发现在抽取检验的2件产品中,其中恰有一件是废品,不可以购买.

【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() “的可以获赠2次随机话费,得分低于
“的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;②若
;②若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
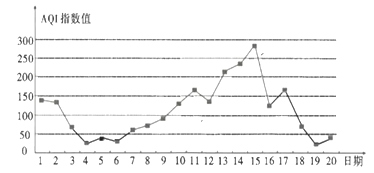
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差