题目内容
【题目】在数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)![]() 的通项公式为__________;
的通项公式为__________;
(2)在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 项中,被
项中,被![]() 除余
除余![]() 的项数为__________.
的项数为__________.
【答案】![]()
![]()
【解析】
(1)根据题意得知数列![]() 为等差数列,确定该数列的首项和公差,可求出数列
为等差数列,确定该数列的首项和公差,可求出数列![]() 的通项公式,即可求出
的通项公式,即可求出![]() ;
;
(2)设![]() ,可得出
,可得出![]() ,由
,由![]() 为奇数,可得出
为奇数,可得出![]() 为
为![]() 的倍数或
的倍数或![]() 为
为![]() 的奇数倍且
的奇数倍且![]() 为偶数,求出两种情况下
为偶数,求出两种情况下![]() 值的个数,相加即可得出答案.
值的个数,相加即可得出答案.
(1)![]() 且
且![]() ,
,
所以,数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公差的等差数列,
为公差的等差数列,
![]() ,
,![]() ;
;
(2)被![]() 整除且余数为
整除且余数为![]() 的整数可表示为
的整数可表示为![]() ,
,
令![]() ,可得
,可得![]() ,
,
![]() ,且
,且![]() ,则
,则![]() 为奇数,
为奇数,
则![]() 为
为![]() 的倍数,或者
的倍数,或者![]() 为
为![]() 的奇数倍且
的奇数倍且![]() 为偶数.
为偶数.
当![]() 为
为![]() 的倍数时,
的倍数时,![]() 的取值有:
的取值有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 个;
个;
当![]() 为
为![]() 的奇数倍且
的奇数倍且![]() 为偶数时,
为偶数时,![]() 的取值有:
的取值有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 个.
个.
综上所述,在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 项中,被
项中,被![]() 除余
除余![]() 的项数为
的项数为![]() .
.
故答案为:![]() ;
;![]() .
.

【题目】已知![]() ,
,![]() . 对于函数
. 对于函数![]() 、
、![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得
,使得![]() ,不等式
,不等式![]() 都成立,则称直线是
都成立,则称直线是![]() 函数
函数![]() 与
与![]() 的分界线.
的分界线.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,试探究函数
时,试探究函数![]() 与
与![]() 是否存在“分界线”?若存在,求出分界线方程;若不存在说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在说明理由.
【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
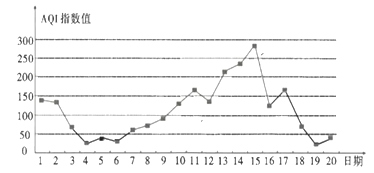
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差
【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
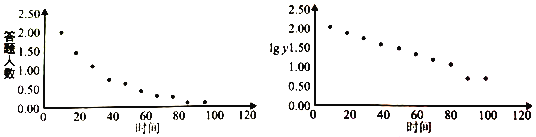
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: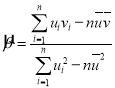 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)