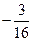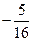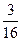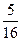题目内容
我们可以运用下面的原理解决一些相关图形的面积问题:如果与一固定直线平行的直线被甲、乙两个封闭图形所截得线段的比为定值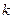 ,那么甲的面积是乙的面积的
,那么甲的面积是乙的面积的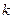 倍,你可以从给出的简单图形①(甲:大矩形
倍,你可以从给出的简单图形①(甲:大矩形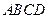 、乙:小矩形
、乙:小矩形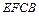 )、②(甲
)、②(甲 :大直角三角形
:大直角三角形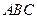 乙:小直角三角形
乙:小直角三角形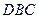 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是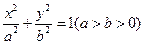 与
与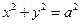 ,运用上面的原理,图③中椭圆的面积为 .
,运用上面的原理,图③中椭圆的面积为 .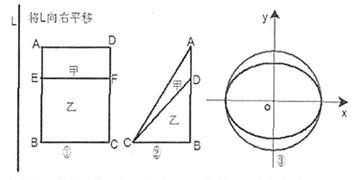
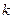 ,那么甲的面积是乙的面积的
,那么甲的面积是乙的面积的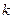 倍,你可以从给出的简单图形①(甲:大矩形
倍,你可以从给出的简单图形①(甲:大矩形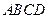 、乙:小矩形
、乙:小矩形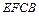 )、②(甲
)、②(甲 :大直角三角形
:大直角三角形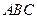 乙:小直角三角形
乙:小直角三角形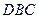 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是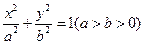 与
与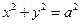 ,运用上面的原理,图③中椭圆的面积为 .
,运用上面的原理,图③中椭圆的面积为 .
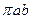
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
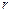 米.市场上,圆柱侧面用料单价为每平方米
米.市场上,圆柱侧面用料单价为每平方米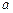 元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为
元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为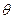 (弧度),总费用为
(弧度),总费用为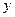 (元).
(元).
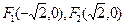 ,平面上动点
,平面上动点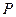 满足
满足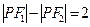 .
.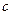 的方程;
的方程;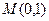 的直线
的直线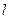 与
与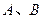 两点,且
两点,且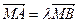 ,当
,当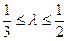 时,求直线
时,求直线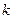 的取值范围.
的取值范围.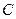 的对称中心为原点O,焦点在
的对称中心为原点O,焦点在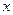 轴上,离心率为
轴上,离心率为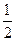 ,且点(1,
,且点(1,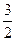 )在该椭圆上.
)在该椭圆上.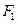 的直线
的直线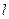 与椭圆
与椭圆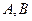 两点,若
两点,若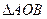 的面积为
的面积为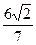 ,求圆心在原点O且与直线
,求圆心在原点O且与直线 程.
程.  与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点. 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程; ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点
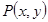 是曲线
是曲线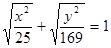 上的点,又点
上的点,又点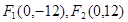 ,下列结
,下列结 .
.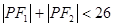 .
. .
. .
. 的离心
的离心 率为
率为 ,该椭圆上一点到两焦点
,该椭圆上一点到两焦点 的距离之和为12,则a=
的距离之和为12,则a=  ,b= 。
,b= 。 的焦点为
的焦点为 ,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 .
,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 .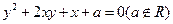 to the y-axis is
to the y-axis is  then the velue of a is
then the velue of a is