题目内容
已知半椭圆 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
(1) 若三角形 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
(2)若“果圆”方程为: ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
(3) 若 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点 的横坐标.
的横坐标.
 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 ,
, 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.(1) 若三角形
 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;(2)若“果圆”方程为:
 ,
, 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围(3) 若
 是“果圆”上任意一点,求
是“果圆”上任意一点,求 取得最小值时点
取得最小值时点 的横坐标.
的横坐标.
(1)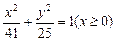 ,
,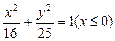
(2)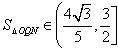
(3)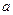 或
或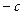
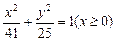 ,
,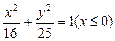
(2)
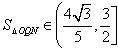
(3)
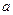 或
或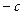
(I)∵
∴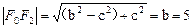 ,
,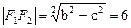 ,
,
于是,c2=16,a2=b2+c2=41,
所求“果圆”方程为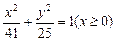 ,
,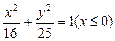
(Ⅱ)①若直线l的斜率k存在,则由图可知,k2>3.设直线l的方程为:y=k(x-1),设点Q,N的坐标分别为(x1,y1),(x2,y2)
由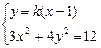 消x,得
消x,得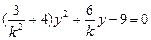
∴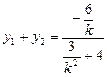 ,
,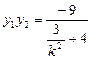
∴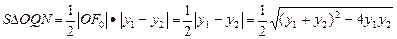

∵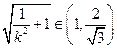
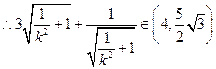
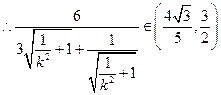
②若直线l⊥x轴,则︱QN︱=3,故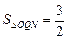
综上,得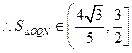
(3)设 是“果圆”的半椭圆
是“果圆”的半椭圆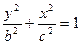
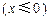 上任意一点.设
上任意一点.设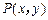 ,则
,则
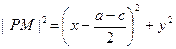
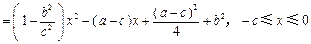 ,
,
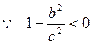 ,
,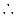
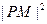 的最小值只能在
的最小值只能在 或
或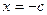 处取到.
处取到.
即当 取得最小值时,
取得最小值时, 在点
在点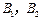 或
或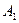 处.
处.
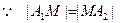 ,且
,且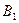 和
和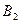 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆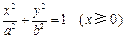 和半椭圆
和半椭圆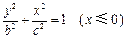 上
上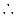 当
当 位于“果圆”的半椭圆
位于“果圆”的半椭圆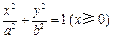 上时.
上时.
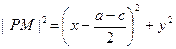
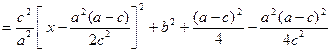 .
.
当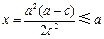 ,即
,即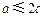 时,
时,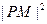 的最小值在
的最小值在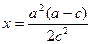 时取到,
时取到,
此时 的横坐标是
的横坐标是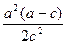 .
.
当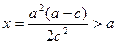 ,即
,即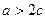 时,由于
时,由于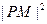 在
在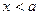 时是递减的,
时是递减的,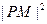 的最小值在
的最小值在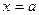 时取到,此时
时取到,此时 的横坐标是
的横坐标是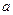 .
.
综上所述,若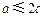 ,当
,当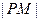 取得最小值时,点
取得最小值时,点 的横坐标是
的横坐标是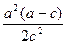 ;若
;若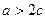 ,当
,当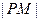 取得最小值时,点
取得最小值时,点 的横坐标是
的横坐标是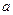 或
或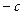 .
.

∴
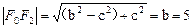 ,
,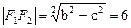 ,
,于是,c2=16,a2=b2+c2=41,
所求“果圆”方程为
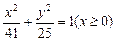 ,
,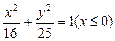
(Ⅱ)①若直线l的斜率k存在,则由图可知,k2>3.设直线l的方程为:y=k(x-1),设点Q,N的坐标分别为(x1,y1),(x2,y2)
由
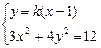 消x,得
消x,得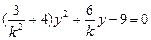
∴
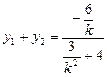 ,
,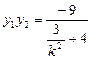
∴
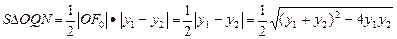

∵
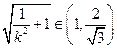
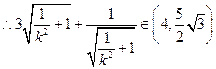
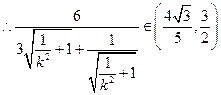
②若直线l⊥x轴,则︱QN︱=3,故
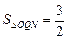
综上,得
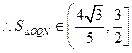
(3)设
 是“果圆”的半椭圆
是“果圆”的半椭圆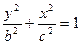
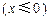 上任意一点.设
上任意一点.设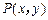 ,则
,则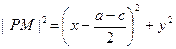
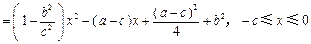 ,
, 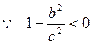 ,
,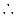
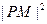 的最小值只能在
的最小值只能在 或
或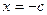 处取到.
处取到.即当
 取得最小值时,
取得最小值时, 在点
在点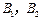 或
或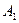 处.
处.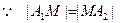 ,且
,且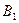 和
和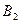 同时位于“果圆”的半椭圆
同时位于“果圆”的半椭圆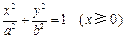 和半椭圆
和半椭圆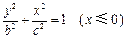 上
上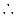 当
当 位于“果圆”的半椭圆
位于“果圆”的半椭圆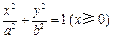 上时.
上时. 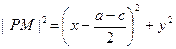
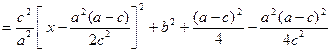 .
.当
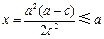 ,即
,即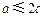 时,
时,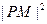 的最小值在
的最小值在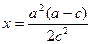 时取到,
时取到,此时
 的横坐标是
的横坐标是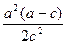 .
. 当
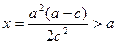 ,即
,即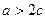 时,由于
时,由于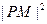 在
在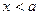 时是递减的,
时是递减的,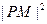 的最小值在
的最小值在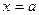 时取到,此时
时取到,此时 的横坐标是
的横坐标是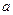 .
. 综上所述,若
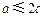 ,当
,当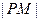 取得最小值时,点
取得最小值时,点 的横坐标是
的横坐标是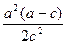 ;若
;若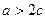 ,当
,当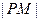 取得最小值时,点
取得最小值时,点 的横坐标是
的横坐标是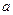 或
或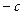 .
.
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
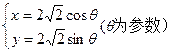 交
交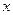 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率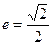 的椭圆。
的椭圆。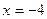 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且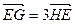 。试求此时弦PQ的长。
。试求此时弦PQ的长。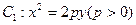 的焦点为F,椭圆
的焦点为F,椭圆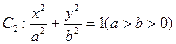 的离心率
的离心率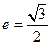 ,C1与C2在第一象限的交点为
,C1与C2在第一象限的交点为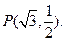
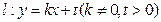 与椭圆C2交于不同两点A、B,点M满足
与椭圆C2交于不同两点A、B,点M满足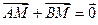 ,直线FM的斜率为k1,试证明
,直线FM的斜率为k1,试证明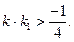
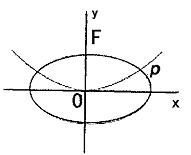
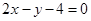 ,则抛物线
,则抛物线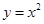 上到直线距离最小的点的坐标为( )
上到直线距离最小的点的坐标为( )
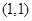


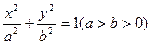 的左右焦点分别为
的左右焦点分别为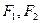 ,短轴两个端点为
,短轴两个端点为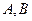 ,且四边形
,且四边形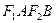 是边长为2的正方形。
是边长为2的正方形。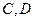 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点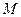 满足
满足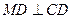 ,连接
,连接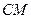 ,交椭圆于
,交椭圆于 点
点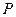 。证明:
。证明: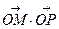 为定值;
为定值;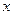 轴上是否存在异于点
轴上是否存在异于点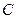 的定点
的定点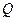 ,使得以
,使得以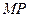 为直径的圆恒过直线
为直径的圆恒过直线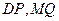 的交点,若存在,求出点
的交点,若存在,求出点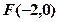 ,则该抛物线的准线方程为 ( )
,则该抛物线的准线方程为 ( )



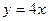 的焦点作直线
的焦点作直线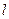 交抛物线于A、B两点,若线段AB中的横坐标为3,则|AB|等于 ( )
交抛物线于A、B两点,若线段AB中的横坐标为3,则|AB|等于 ( )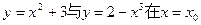 处的切线互相垂直,则
处的切线互相垂直,则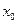 的值为 .
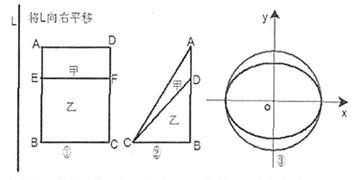
的值为 .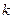 ,那么甲的面积是乙的面积的
,那么甲的面积是乙的面积的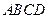 、乙:小矩形
、乙:小矩形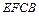 )、②(甲
)、②(甲 :大直角三角形
:大直角三角形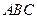 乙:小直角三角形
乙:小直角三角形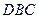 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是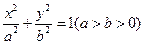 与
与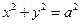 ,运用上面的原理,图③中椭圆的面积为 .
,运用上面的原理,图③中椭圆的面积为 .