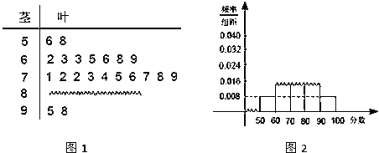题目内容
【题目】某企业质量检验员为了检测生产线上零件的质量情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:

(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)若从这![]() 个零件中尺寸位于
个零件中尺寸位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个,设
个,设![]() 表示尺寸在
表示尺寸在![]() 上的零件个数,求
上的零件个数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)已知尺寸在![]() 上的零件为一等品,否则为二等品,将这
上的零件为一等品,否则为二等品,将这![]() 个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱
个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱![]() 个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为
个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为![]() 元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付
元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付![]() 元的赔偿费用. 现对一箱零件随机抽检了
元的赔偿费用. 现对一箱零件随机抽检了![]() 个,结果有
个,结果有![]() 个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
【答案】(1)![]() ;(2)分布列见详解,期望为
;(2)分布列见详解,期望为![]() ;(3)余下所有零件不用检验,理由见详解.
;(3)余下所有零件不用检验,理由见详解.
【解析】
(1)计算![]() 的频率,并且与
的频率,并且与![]() 进行比较,判断中位数落在的区间,然后根据频率的计算方法,可得结果.
进行比较,判断中位数落在的区间,然后根据频率的计算方法,可得结果.
(2)计算位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个的总数,写出
个的总数,写出![]() 所有可能取值,并计算相对应的概率,列出分布列,计算期望,可得结果.
所有可能取值,并计算相对应的概率,列出分布列,计算期望,可得结果.
(3)计算整箱的费用,根据余下零件个数服从二项分布,可得余下零件个数的期望值,然后计算整箱检验费用与赔偿费用之和的期望值,进行比较,可得结果.
(1)尺寸在![]() 的频率:
的频率:
![]()
尺寸在![]() 的频率:
的频率:![]()
且![]()
所以可知尺寸的中位数落在![]()
假设尺寸中位数为![]()
所以![]()
所以这![]() 个零件尺寸的中位数
个零件尺寸的中位数![]()
(2)尺寸在![]() 的个数为
的个数为![]()
尺寸在![]() 的个数为
的个数为![]()
![]() 的所有可能取值为1,2,3,4
的所有可能取值为1,2,3,4
则![]() ,
,![]()
![]() ,
,![]()
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]()
(3)二等品的概率为![]()
如果对余下的零件进行检验则整箱的检验费用为
![]() (元)
(元)
余下二等品的个数期望值为![]()
如果不对余下的零件进行检验,
整箱检验费用与赔偿费用之和的期望值为
![]() (元)
(元)
所以![]() ,所以可以不对余下的零件进行检验.
,所以可以不对余下的零件进行检验.

 备战中考寒假系列答案
备战中考寒假系列答案