题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)对任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() (2)函数
(2)函数![]() 取得最大值
取得最大值![]() (3)
(3)![]()
【解析】
(1)将![]() 代入函数,去掉绝对值得到分段函数,然后分别求导,利用导数求函数的单调区间.
代入函数,去掉绝对值得到分段函数,然后分别求导,利用导数求函数的单调区间.
(2)![]() ,则
,则![]() ,对函数求导,判断单调性,根据单调性即可得出函数在区间
,对函数求导,判断单调性,根据单调性即可得出函数在区间![]() 上的最大值.
上的最大值.
(3)由(1)(2)得,![]() ,分情况讨论
,分情况讨论![]() 、
、![]() 时函数的单调性,从而得出实数
时函数的单调性,从而得出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时, 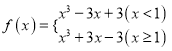 ,
,
若![]() 时,则
时,则![]() ,令
,令![]() ,解得
,解得![]() ;
;
若![]() 时,则
时,则![]() 恒成立,所以
恒成立,所以![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)若![]() ,当
,当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,解得
,解得![]() 或
或![]() .
.
列表如下:
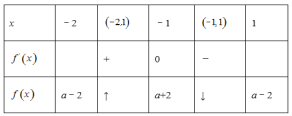
当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .
.
(3)由(1)(2)得,![]() .
.
①当![]() 时,即
时,即![]() 时,
时,
![]() ,即
,即![]() .
.
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,
,
所以![]() ,解得
,解得![]() ,又
,又![]() ,所以
,所以![]() .
.
②当![]() 即
即![]() 时,
时,
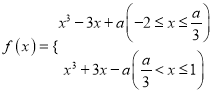
当![]() 时,
时,![]() ,即
,即![]() ,
,
与![]() 矛盾,
矛盾,
所以,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某企业积极响应国家“科技创新”的号召,大力研发人工智能产品,为了对一批新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]()
![]() ,如下表所示:
,如下表所示:
试销单价 | 1 | 2 | 3 | 4 | 5 | 6 |
产品销量 | 91 | 86 |
| 78 | 73 | 70 |
附:参考公式: ,
,![]() ,
,
参考数据:![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)已知变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (百元)的线性回归方程
(百元)的线性回归方程![]() (计算结果精确到整数位);
(计算结果精确到整数位);
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据称为一个“有效数据”.现从这6组销售数据中任取2组,求抽取的2组销售数据都是“有效数据”的概率.
时,则将销售数据称为一个“有效数据”.现从这6组销售数据中任取2组,求抽取的2组销售数据都是“有效数据”的概率.