ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Η÷≥ߥρΥψΉβ”Ο![]() Θ§
Θ§ ![]() ΝΫ÷÷–ΆΚ≈ΒΡΜπ≥Β≥ΒΤΛ‘Υ δ900Ε÷Η÷≤ΡΘ§
ΝΫ÷÷–ΆΚ≈ΒΡΜπ≥Β≥ΒΤΛ‘Υ δ900Ε÷Η÷≤ΡΘ§ ![]() Θ§
Θ§ ![]() ΝΫ÷÷≥ΒΤΛΒΡ‘ΊΜθΝΩΖ÷±πΈΣ36Ε÷ΚΆ60Ε÷Θ§ΉβΫπΖ÷±πΈΣ1.6Άρ‘Σ/ΗωΚΆ2.4Άρ‘Σ/ΗωΘ§Η÷≥ß“Σ«σΉβ≥ΒΤΛΉή ΐ≤Μ≥§Ιΐ21ΗωΘ§«“
ΝΫ÷÷≥ΒΤΛΒΡ‘ΊΜθΝΩΖ÷±πΈΣ36Ε÷ΚΆ60Ε÷Θ§ΉβΫπΖ÷±πΈΣ1.6Άρ‘Σ/ΗωΚΆ2.4Άρ‘Σ/ΗωΘ§Η÷≥ß“Σ«σΉβ≥ΒΤΛΉή ΐ≤Μ≥§Ιΐ21ΗωΘ§«“![]() –Ά≥ΒΤΛ≤ΜΕύ”Ύ
–Ά≥ΒΤΛ≤ΜΕύ”Ύ![]() –Ά≥ΒΤΛ7ΗωΘ§Ζ÷±π”Ο
–Ά≥ΒΤΛ7ΗωΘ§Ζ÷±π”Ο![]() Θ§
Θ§ ![]() ±μ ΨΉβ”Ο
±μ ΨΉβ”Ο![]() Θ§
Θ§ ![]() ΝΫ÷÷≥ΒΤΛΒΡΗω ΐ.
ΝΫ÷÷≥ΒΤΛΒΡΗω ΐ.
Θ®ΔώΘ©”Ο![]() Θ§
Θ§ ![]() Ν–≥ω¬ζΉψΧθΦΰΒΡ ΐ―ßΙΊœΒ ΫΘ§≤ΔΜ≠≥ωœύ”ΠΒΡΤΫΟφ«χ”ρΘΜ
Ν–≥ω¬ζΉψΧθΦΰΒΡ ΐ―ßΙΊœΒ ΫΘ§≤ΔΜ≠≥ωœύ”ΠΒΡΤΫΟφ«χ”ρΘΜ
Θ®ΔρΘ©Ζ÷±πΉβ”Ο![]() Θ§
Θ§ ![]() ΝΫ÷÷≥ΒΤΛΒΡΗω ΐ «Εύ…Ό ±Θ§≤≈Ρή ΙΒΟΉβΫπΉν…ΌΘΩ≤Δ«σ≥ω¥ΥΉν–ΓΉβΫπ.
ΝΫ÷÷≥ΒΤΛΒΡΗω ΐ «Εύ…Ό ±Θ§≤≈Ρή ΙΒΟΉβΫπΉν…ΌΘΩ≤Δ«σ≥ω¥ΥΉν–ΓΉβΫπ.
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©ΦϊΫβΈω; Θ®ΔρΘ©Ζ÷±πΉβ”Ο![]() ΓΔ
ΓΔ![]() ΝΫ÷÷≥ΒΤΛ5ΗωΘ§12Ηω ±ΉβΫπΉν–ΓΘ§«“Ήν–ΓΉβΫπΈΣ36.8Άρ.
ΝΫ÷÷≥ΒΤΛ5ΗωΘ§12Ηω ±ΉβΫπΉν–ΓΘ§«“Ήν–ΓΉβΫπΈΣ36.8Άρ.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
Θ®ΔώΘ©”…“―÷ΣΧθΦΰΝ–≥ω![]() ΒΡ‘Φ χΧθΦΰΘ§Ω…Μ≠≥ωΩ…––”ρΘΜ
ΒΡ‘Φ χΧθΦΰΘ§Ω…Μ≠≥ωΩ…––”ρΘΜ
Θ®ΔρΘ©«σ≥ωΡΩ±ξΚ· ΐΈΣ![]() Θ§Ής÷±œΏ
Θ§Ής÷±œΏ![]() Θ§“Ή÷Σœρ…œΤΫ“Τ÷±œΏ
Θ§“Ή÷Σœρ…œΤΫ“Τ÷±œΏ![]() ±Θ§
±Θ§ ![]() ‘ω¥σΘ§¥”ΕχΩ…ΒΟΉν”≈ΫβΘ°
‘ω¥σΘ§¥”ΕχΩ…ΒΟΉν”≈ΫβΘ°
‘ΧβΫβΈωΘΚ
Θ®ΔώΘ©”…“―÷Σ![]() Θ§
Θ§ ![]() ¬ζΉψΒΡ ΐ―ßΙΊœΒ ΫΈΣ
¬ζΉψΒΡ ΐ―ßΙΊœΒ ΫΈΣ

ΗΟΕΰ‘Σ“Μ¥Έ≤ΜΒ» ΫΉιΥυ±μ ΨΒΡΤΫΟφ«χ”ρΈΣΆΦ÷–“θ”Α≤ΩΖ÷Υυ Ψ.
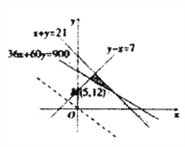
Θ®ΔρΘ©…ηΉβΫπΈΣ![]() ‘ΣΘ§‘ρΡΩ±ξΚ· ΐ
‘ΣΘ§‘ρΡΩ±ξΚ· ΐ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§’β «–±¬ ΈΣ
Θ§’β «–±¬ ΈΣ![]() .‘Ύ
.‘Ύ![]() ÷α…œΒΡΫΊΨύΈΣ
÷α…œΒΡΫΊΨύΈΣ![]() ΒΡ“ΜΉεΤΫ––÷±œΏ.
ΒΡ“ΜΉεΤΫ––÷±œΏ.
Β±![]() »ΓΉν–Γ÷Β ±Θ§
»ΓΉν–Γ÷Β ±Θ§ ![]() ΒΡ÷ΒΉν–ΓΘ§”÷“ρΈΣ
ΒΡ÷ΒΉν–ΓΘ§”÷“ρΈΣ![]() Θ§
Θ§ ![]() ¬ζΉψ‘Φ χΧθΦΰΘ§Υυ“‘”…ΆΦΩ…÷ΣΘ§Β±÷±œΏ
¬ζΉψ‘Φ χΧθΦΰΘ§Υυ“‘”…ΆΦΩ…÷ΣΘ§Β±÷±œΏ![]() Ψ≠ΙΐΩ…––”ρ÷–ΒΡΒψ
Ψ≠ΙΐΩ…––”ρ÷–ΒΡΒψ![]() ±Θ§ΫΊΨύ
±Θ§ΫΊΨύ![]() ΒΡ÷ΒΉν–ΓΘ§Φ¥
ΒΡ÷ΒΉν–ΓΘ§Φ¥![]() ΒΡ÷ΒΉν–Γ.
ΒΡ÷ΒΉν–Γ.
ΫβΖΫ≥ΧΉι![]() Θ§ΒΟΒψ
Θ§ΒΟΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() .
.
Υυ“‘![]() Θ®Άρ‘ΣΘ©.
Θ®Άρ‘ΣΘ©.
¥πΘΚΖ÷±πΉβ”Ο![]() ΓΔ
ΓΔ![]() ΝΫ÷÷≥ΒΤΛ5ΗωΘ§12Ηω ±ΉβΫπΉν–ΓΘ§«“Ήν–ΓΉβΫπΈΣ36.8Άρ.
ΝΫ÷÷≥ΒΤΛ5ΗωΘ§12Ηω ±ΉβΫπΉν–ΓΘ§«“Ήν–ΓΉβΫπΈΣ36.8Άρ.