Question

【题目】已知圆C的半径为2，圆心在轴的正半轴上，直线与圆C相切.

（1）求圆C的方程；

（2）过点的直线与圆C交于不同的两点，且当时，求的面积.

Answer 1

【答案】（1）+（2）

【解析】试题分析：（I）设圆心为C（a，0），（a＞0），可得圆C的方程的方程．再根据圆心到直线的距离等于半径求得a的值，可得圆C的方程．

（II）依题意：设直线l的方程为：y=kx﹣3，代入圆的方程化简，利用根与系数的关系求得两根和与两根积，再由x1x2+y1y2=3，求得k的值，可得∴直线l的方程．求得圆心C到l的距离d、以及|AB|的值，再由面积公式，计算求得结果．

试题解析：

（1）设圆心为，则圆C的方程为

因为圆C与相切 所以 解得：（舍）

所以圆C的方程为：

（2）依题意：设直线l的方程为：

由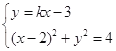得

∵l与圆C相交于不同两点

∴

又∵ ∴

整理得： 解得（舍）

∴直线l的方程为：

圆心C到l的距离 在△ABC中，|AB|=

原点O到直线l的距离，即△AOB底边AB边上的高

∴