题目内容
【题目】已知函数f(x)=2 ![]() .
.
(1)求函数f(x)的定义域和值域;
(2)求函数f(x)的单调区间.
【答案】
(1)解:对于函数f(x)=2 ![]() ,
,
令t=x2﹣2x﹣3=(x﹣1)2﹣4≥﹣4,可得f(x)=g(t)=2t (t≥﹣4).
由于t的定义域为R,故故函数的定义域为R.
∵t≥﹣4,故f(x)≥2﹣4= ![]() ,故f(x)的值域为[
,故f(x)的值域为[ ![]() ,+∞).
,+∞).
(2)解:根据f(x)=g(t)=2t,函数f(x)的单调区间,即函数t的单调区间.
由于函数t=(x﹣1)2﹣4的减区间为(﹣∞,1],增区间为:[1,+∞),
故函数f(x)的单调递减区间:(﹣∞,1],单调递增区间:[1,+∞)
【解析】(1)令t=x2﹣2x﹣3,f(x)=g(t)=2t (t≥﹣4),利用二次函数的性质求得t的定义域与值域,可得函数f(x)的定义域和值域.(2)函数f(x)的单调区间,即函数t的单调区间,再利用二次函数的性质得出结论.
【考点精析】关于本题考查的函数的定义域及其求法和函数的值域,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
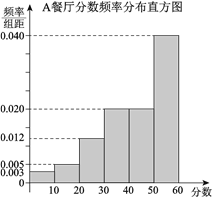
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.