题目内容
10.已知数列{an}的通项公式为an=pn+$\frac{q}{n}$,且a2=$\frac{3}{2}$,a4=$\frac{3}{2}$,则a8=$\frac{9}{4}$.分析 an=pn+$\frac{q}{n}$,且a2=$\frac{3}{2}$,a4=$\frac{3}{2}$,代入$\left\{\begin{array}{l}{2p+\frac{q}{2}=\frac{3}{2}}\\{4p+\frac{q}{4}=\frac{3}{2}}\end{array}\right.$,解出即可得出.
解答 解:∵an=pn+$\frac{q}{n}$,且a2=$\frac{3}{2}$,a4=$\frac{3}{2}$,
∴$\left\{\begin{array}{l}{2p+\frac{q}{2}=\frac{3}{2}}\\{4p+\frac{q}{4}=\frac{3}{2}}\end{array}\right.$,
解得p=$\frac{1}{4}$,q=2,
∴an=$\frac{1}{4}n+\frac{2}{n}$.
则a8=$\frac{1}{4}×8+\frac{2}{8}$=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了待定系数法求数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列说法正确的是( )
| A. | 铺的很平的一张白纸是一个平面 | B. | 平面是矩形或平行四边形的形状 | ||
| C. | 两个平面叠在一起比一个平面厚 | D. | 平面的直观图一般画成平行四边形 |
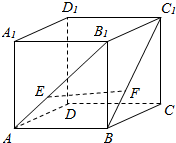 如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)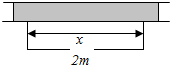 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).