题目内容
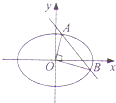
【题目】设A1、A2为椭圆 ![]() 的左右顶点,若在椭圆上存在异于A1、A2的点P,使得
的左右顶点,若在椭圆上存在异于A1、A2的点P,使得 ![]() ,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:A1(﹣a,0),A2(a,0),设P(x,y),则 ![]() =(﹣x,﹣y),
=(﹣x,﹣y), ![]() =(a﹣x,﹣y),
=(a﹣x,﹣y),
∵ ![]() ,∴(a﹣x)(﹣x)+(﹣y)(﹣y)=0,y2=ax﹣x2>0,∴0<x<a.
,∴(a﹣x)(﹣x)+(﹣y)(﹣y)=0,y2=ax﹣x2>0,∴0<x<a.
代入 ![]() =1,整理得(b2﹣a2)x2+a3x﹣a2b2=0 在(0,a )上有解,
=1,整理得(b2﹣a2)x2+a3x﹣a2b2=0 在(0,a )上有解,
令f(x)=(b2﹣a2)x2+a3x﹣a2b2=0,∵f(0)=﹣a2b2<0,f(a)=0,如图:
△=(a3)2﹣4×(b2﹣a2)×(﹣a2b2)=a2( a4﹣4a2b2+4b4 )=a2(a2﹣2b2)2≥0,
∴对称轴满足 0<﹣ ![]() <a,即 0<
<a,即 0< ![]() <a,∴
<a,∴ ![]() <1,
<1,![]() >
> ![]() ,又 0<
,又 0< ![]() <1,∴
<1,∴ ![]() <
< ![]() <1,故选 D.
<1,故选 D.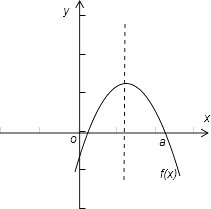

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目